题目内容
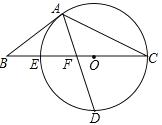
【题目】如图，点E在直线BH、DC之间，点A为BH上一点，且AE⊥CE， 
.
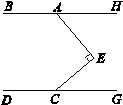
（1）求证：BH∥CD；
（2）如图：直线AF交DC于F，AM平分∠EAF，AN平分∠BAE. 试探究∠MAN，∠AFG的数量关系.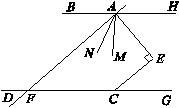
【答案】
（1）解：延长AE交DC于点F
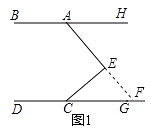
∵∠DCE=∠EFC+90°， 
∴∠HAE=∠EFC
∴BH∥CD；
（2）解：∵BH∥CD
∴∠BAF=∠AFG
∵AM平分∠EAF，AN平分∠BAE
∴∠MAN＝∠EAN-∠EAM= 
（∠BAE-∠EAF）= ∠BAF
∴∠MAN＝ ∠AFG
【解析】（1）通过延长构造出第三条直线，进而构造出内错角，利用外角定理证出内错角相等，进而证出平行；（2）利用平行线的性质和平分线的定义可证出结论.
练习册系列答案
相关题目
【题目】某校随机抽查了10名参加2016年云南省初中学业水平考试学生的体育成绩，得到的结果如表：
成绩（分） | 46 | 47 | 48 | 49 | 50 |
人数（人） | 1 | 2 | 1 | 2 | 4 |
下列说法正确的是（ ）
A.这10名同学的体育成绩的众数为50
B.这10名同学的体育成绩的中位数为48
C.这10名同学的体育成绩的方差为50
D.这10名同学的体育成绩的平均数为48
