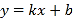��Ŀ����
����Ŀ���������С��ÿ��С������ֱ����1��2��3��4��5����������е�һ������ЩС���������ֲ�ͬ���⣬�����ȫ����ͬ���ѷֱ��������4��5������С����벻���Ŀڴ� A �У��ѷֱ��������1��2��3������С����벻���Ŀڴ� B �У�������� A �� B �����ڴ��и�ȡ��һ��С�Ѵ� A �ڴ���ȡ����С���ϱ�����ּ��� m���� B �ڴ���ȡ����С���ϱ�����ּ���n����m��n=k�������x��һԪ���η���2x2��4x+k=0�н�ĸ����� ��
���𰸡�![]()
���������⣺����״ͼ���£�
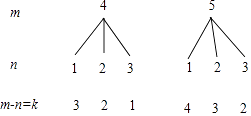
�߹���x��һԪ���η���2x2��4x+k=0�н⣬
���=16��8k��0����k��2��
�����x��һԪ���η���2x2��4x+k=0�н�ĸ����� ![]() =
= ![]() ��
��
�����㾫�������������ʽ���б�������״ͼ������Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪�����б�ʽ��=b2-4ac��������Է�Ϊ3�������1������>0ʱ��һԪ���η�����2������ȵ�ʵ����2������=0ʱ��һԪ���η�����2����ͬ��ʵ����3������<0ʱ��һԪ���η���û��ʵ��������һ������Ҫ�����������������ʱ�����б����Ͳ������ˣ�Ϊ�˲��ز�©���г����п��ܵĽ����ͨ��������״ͼ������ʣ�