题目内容
CD为Rt△ABC斜边上的高线,AC、BC为x2-5x+2=0的两根,则AD•BD的值等于分析:先由根与系数的关系得出,AC•BD=2,再证明△ACD∽△CBD,则
=
,化为乘积式即可得出AD•BD=CD2,再根据三角形的面积得出CD即可.
| AD |
| CD |
| CD |
| BD |
解答:解:∵AC、BC为x2-5x+2=0的两根,
∴AC+BC=5,AC•BC=2,
∴AB=
=
=
,
∵∠A+∠ACDE=90°,∠BCD+∠ACD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD,
∴
=
,
即AD•BD=CD2,
∵AC•BC=AB•CD,
∴CD=
=
=
,
∴AD•BD=CD2=
,
故答案为
.
∴AC+BC=5,AC•BC=2,
∴AB=
| AC2+BC2 |
| (AC+BC)2-2AC•BC |
| 21 |
∵∠A+∠ACDE=90°,∠BCD+∠ACD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD,
∴
| AD |
| CD |
| CD |
| BD |
即AD•BD=CD2,
∵AC•BC=AB•CD,
∴CD=
| AC•BC |
| AB |
| 2 | ||
|
2
| ||
| 21 |
∴AD•BD=CD2=
| 4 |
| 21 |
故答案为
| 4 |
| 21 |
点评:本题考查了根与系数的关系、相似三角形的判定和性质,直角三角形的面积公式.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
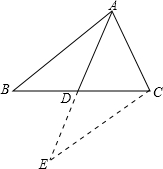 阅读并解答问题.
阅读并解答问题.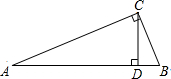 已知:CD为Rt△ABC的斜边上的高,且BC=a,AC=b,AB=c,CD=h(如图).求证:
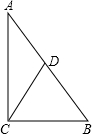
已知:CD为Rt△ABC的斜边上的高,且BC=a,AC=b,AB=c,CD=h(如图).求证: 如图,CD为Rt△ABC的斜边AB上的高线,∠BAC的平分线交BC,CD于点E,F,求证:△ABE∽△ACF.
如图,CD为Rt△ABC的斜边AB上的高线,∠BAC的平分线交BC,CD于点E,F,求证:△ABE∽△ACF.