题目内容
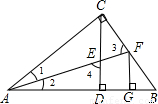
 如图,CD为Rt△ABC的斜边AB上的高线,∠BAC的平分线交BC,CD于点E,F,求证:△ABE∽△ACF.
如图,CD为Rt△ABC的斜边AB上的高线,∠BAC的平分线交BC,CD于点E,F,求证:△ABE∽△ACF.分析:根据直角三角形两锐角互余和CD是斜边上的高可以得到∠ACD=∠B,再根据AE是∠BAC的平分线可以得到∠CAE=∠EAB,利用两角对应相等,两三角形相似即可证明;
解答:证明:∵∠ACB=90°,∠CDB=90°,
∴∠ACD=90°-∠DCB,∠B=90°-∠DCB,
∴∠ACD=∠B,
∵AE平分∠CAB,
∴∠CAE=∠EAB,
∴△ACF∽△ABE.
∴∠ACD=90°-∠DCB,∠B=90°-∠DCB,
∴∠ACD=∠B,
∵AE平分∠CAB,
∴∠CAE=∠EAB,
∴△ACF∽△ABE.
点评:本题考查了相似三角形的判定.解答本题需要熟练掌握相似三角形的判定方法和相似三角形的对应边成比例.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 6、如图,CD为Rt△ABC斜边上的高,∠BAC的平分线分别交CD、CB于点E、F,FG⊥AB,垂足为G,则CF
6、如图,CD为Rt△ABC斜边上的高,∠BAC的平分线分别交CD、CB于点E、F,FG⊥AB,垂足为G,则CF
 如图,CD为Rt△ABC的斜边AB上的高线,∠BAC的平分线交BC,CD于点E,F,求证:△ABE∽△ACF.
如图,CD为Rt△ABC的斜边AB上的高线,∠BAC的平分线交BC,CD于点E,F,求证:△ABE∽△ACF.