��Ŀ����
 �Ķ���������⣮
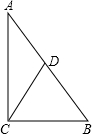
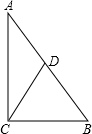
�Ķ���������⣮��ͼ����֪��ADΪ��ABC�����ߣ���֤��AB+AC��2AD��
֤�����ӳ�AD��Eʹ��DE=AD������EC����AE=2AD
��AD��ABC������
��BD=CD
�ڡ�ABD�͡�CED��
|
���ABD�ա�CED
��AB=EC
�ڡ�ACE�У����������ε����߹�ϵ��
AC+EC
��AB=EC��AE=2AD
��AB+AC��2AD
���ָ����߷��������dz�Ϊ���������߷��������������ַ�������������⣺
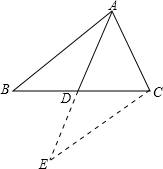
��1����ͼ����֪��CDΪRt��ABC�����ߣ���ACB=90�㣬��֤��CD=
| 1 |
| 2 |
��2���ѣ�1���еĽ����ü�����������������
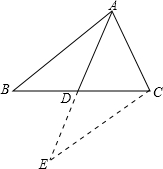
��������1���ӳ�CD��EʹDE=CD������EB��AE����֤��ADC�ա�BDE����AC=BE���ı���ACBE��ƽ���ı��Σ������ó�ƽ���ı���ACBE�Ǿ��Σ���AB=CE=2CD��
��2������֤���Ľ��۵ó�ֱ��������б���ϵ����ߵ���б�ߵ�һ�룮
��2������֤���Ľ��۵ó�ֱ��������б���ϵ����ߵ���б�ߵ�һ�룮
��� �⣺��1��֤�����ӳ�CD��EʹDE=CD������EB��AE��
�⣺��1��֤�����ӳ�CD��EʹDE=CD������EB��AE��
��CDΪRt��ABC�����ߣ�
��AD=CD��
��CD=DE����ADC=��EDB��
���ADC�ա�EDB��
���ACD=��DEB��AC=BE��
��AC��BE��
���ı���ACBE��ƽ���ı��Σ�
�֡ߡ�ACB=90�㣬
��ƽ���ı���ACBE�Ǿ��Σ�
��AB=CE��CD=DE=AD=BD��
��CD=
AB��
��2��ֱ��������б���ϵ����ߵ���б�ߵ�һ�룮
 �⣺��1��֤�����ӳ�CD��EʹDE=CD������EB��AE��
�⣺��1��֤�����ӳ�CD��EʹDE=CD������EB��AE����CDΪRt��ABC�����ߣ�
��AD=CD��
��CD=DE����ADC=��EDB��
���ADC�ա�EDB��
���ACD=��DEB��AC=BE��
��AC��BE��
���ı���ACBE��ƽ���ı��Σ�
�֡ߡ�ACB=90�㣬
��ƽ���ı���ACBE�Ǿ��Σ�
��AB=CE��CD=DE=AD=BD��
��CD=
| 1 |
| 2 |
��2��ֱ��������б���ϵ����ߵ���б�ߵ�һ�룮
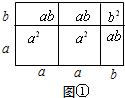
������������Ҫ������ȫ�������ε��ж��������Լ����ε��ж������ʵ�֪ʶ��������֪�ó�AB=CE���þ������ʵó��ǽ������Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ

 �Ķ���������⣮
�Ķ���������⣮ ��
�� ��
�� ��
�� ��
��
