题目内容
已知二次函数的图象经过A(2,0)、C(0,12)两点,且对称轴为直线x=4,设顶点为点P,与x轴的另一交点为点B。

(1)求二次函数的解析式及顶点P的坐标;
(2)如图1,在直线y=2x上是否存在点D,使四边形OPBD为等腰梯形?若存在,求出点D的坐标;若不存在,请说明理由;
(3)如图2,点M是线段OP上的一个动点(O、P两点除外),以每秒 个单位长度的速度由点P向点O运动,过点M作直线MN∥x轴,交PB于点N,将△PMN沿直线MN对折,得到△P1MN,在动点M的运动过程中,设△P1MN与梯形OMNB的重叠部分的面积为S,运动时间为t秒,求S关于t的函数关系式。
个单位长度的速度由点P向点O运动,过点M作直线MN∥x轴,交PB于点N,将△PMN沿直线MN对折,得到△P1MN,在动点M的运动过程中,设△P1MN与梯形OMNB的重叠部分的面积为S,运动时间为t秒,求S关于t的函数关系式。
(2)如图1,在直线y=2x上是否存在点D,使四边形OPBD为等腰梯形?若存在,求出点D的坐标;若不存在,请说明理由;
(3)如图2,点M是线段OP上的一个动点(O、P两点除外),以每秒
 个单位长度的速度由点P向点O运动,过点M作直线MN∥x轴,交PB于点N,将△PMN沿直线MN对折,得到△P1MN,在动点M的运动过程中,设△P1MN与梯形OMNB的重叠部分的面积为S,运动时间为t秒,求S关于t的函数关系式。
个单位长度的速度由点P向点O运动,过点M作直线MN∥x轴,交PB于点N,将△PMN沿直线MN对折,得到△P1MN,在动点M的运动过程中,设△P1MN与梯形OMNB的重叠部分的面积为S,运动时间为t秒,求S关于t的函数关系式。解:(1)设二次函数的解析式为y=ax2+bx+c
由题意得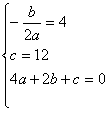
解得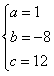
∴二次函数的解析式为y=x2-8x+12,
点P的坐标为(4,-4)。
(2)存在点D,使四边形OPBD为等腰梯形
理由如下:当y=0时,x2-8x+12=0
∴x1=2,x2=6
∴点B的坐标为(6,0)
设直线BP的解析式为y=kx+m
则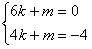
解得
∴直线BP的解析式为y=2x-12
∴直线OD∥BP
∵顶点坐标P(4, -4)
∴OP=4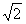
设D(x,2x)
则BD2=(2x)2+(6-x)2
当BD=OP时,(2x)2+(6-x)2=32
解得:x1=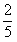 ,x2=2
,x2=2
当x2=2时,OD=BP=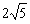 ,四边形OPBD为平行四边形,舍去
,四边形OPBD为平行四边形,舍去
∴当x= 时四边形OPBD为等腰梯形
时四边形OPBD为等腰梯形
∴当D(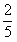 ,
,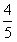 )时,四边形OPBD为等腰梯形。
)时,四边形OPBD为等腰梯形。
(3)① 当0<t≤2时,
∵运动速度为每秒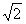 个单位长度,运动时间为t秒,
个单位长度,运动时间为t秒,
则MP=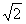 t
t
∴PH=t,MH=t,HN= t
t
∴MN=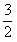 t
t
∴S=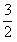 t·t·
t·t·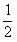 =
=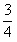 t2;
t2;
②当2<t<4时,P1G=2t-4,P1H=t
∵MN∥OB
∴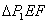 ∽
∽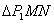
∴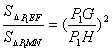
∴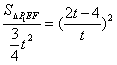
∴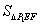 =3t2-12t+12
=3t2-12t+12
∴S=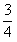 t2-(3t2-12t+12)=-
t2-(3t2-12t+12)=-![]() t2+12t-12
t2+12t-12
∴ 当0<t≤2时,S=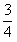 t2
t2
当2<t<4时,S=-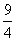 t2+12t-12。
t2+12t-12。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目