��Ŀ����
����Ŀ�����������
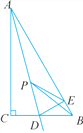
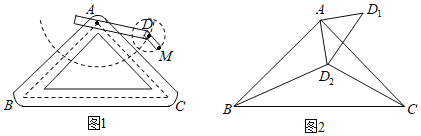
(1)��ͼ�٣���������![]() �У�
��![]() ����
����![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ϣ�����
�ϣ�����![]() ����
����![]() ��
��![]() ����
����![]() Ϊб�ߣ�������ֱ��������
Ϊб�ߣ�������ֱ��������![]() �����ڱ�
�����ڱ�![]() �ϴ��� ������������ֱ�Ƕ���
�ϴ��� ������������ֱ�Ƕ���![]() ��
��
����̽����
(2)��ͼ�ڣ���(1)�������£�![]() �Ƿ��������һ��ֱ��������
�Ƿ��������һ��ֱ��������![]() ����
����![]() �������
�������
��������
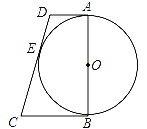
(3)ijС����һ���߳�Ϊ40�������λ����С����ҵ��һ��ǽ��![]() ����װ̨��������ü�������ӽ�Ϊ
����װ̨��������ü�������ӽ�Ϊ![]() �������������������ת�������ҿ��Լ�ظ������ÿһ���ط�����ͼ�ۣ�������
�������������������ת�������ҿ��Լ�ظ������ÿһ���ط�����ͼ�ۣ�������![]() �ǹ���
�ǹ���![]() ��һ��ˮƽ�棬
��һ��ˮƽ�棬![]() ��
��![]() ��������
��������![]() ��ͬһ��ƽ���ڣ�����
��ͬһ��ƽ���ڣ�����![]() ����
����![]() Ϊ
Ϊ![]()
![]() �������ֵ��
�������ֵ��
���𰸡�(1)2;(2)![]() ;(3)
;(3) ![]() ��������ֵΪ500����СֵΪ400.
��������ֵΪ500����СֵΪ400.
��������
(1) ��F��FH��DC��DC�ཻ��H,��BE=x���ֱ���Rt��GHF��Rt��BEF��Rt��ECG���ù��ɶ�����ʾFE2��EG2��FG2,����BC�ϴ��ڵ�Eʹ��![]() Ϊֱ�������Σ���������
Ϊֱ�������Σ���������![]() ��������ʽ��ΪһԪ���η��̣����ݷ��̵Ľ��������������ж������ĵ���������
��������ʽ��ΪһԪ���η��̣����ݷ��̵Ľ��������������ж������ĵ���������
��2�����ݣ�1���п����BE=1���ֱ����EF��EG�������![]() �������
�������
��3����G��AD�Ϻ�G��CD�������������.�ɽ������������ʾ![]() �����������a��ȡֵ��Χ�ɷֱ�
�����������a��ȡֵ��Χ�ɷֱ�![]() �����������ֵ����Сֵ.
�����������ֵ����Сֵ.
(1)��ͼ��F��FH��DC��DC�ཻ��H��
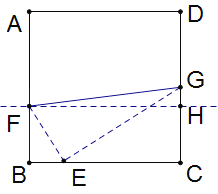
���FHC=��FHG=90��
���ı���![]() Ϊ�����Σ�
������
���B=��C=90����BC=AD=4��
���ı���![]() Ϊ���Σ�
����
��![]() ,FH=BC=4.
,FH=BC=4.
��![]() ��
��
��![]()
��Rt��GHG�и��ݹ��ɶ���
![]() .
.
����BC�ϴ���E����BE=x����EC=4-x.
����Rt��BEF��Rt��ECG�и��ݹ��ɶ���
![]() ��
��
![]() .
.
Ҫʹ��EFGΪֱ�������Σ�����ݹ��ɶ������涨��
![]() ��
��![]()
�����![]()
��![]()
��÷�������������ȵĽ⣬������������E��������
���2.
��2����![]() ��
��![]()
��![]()
��BE=1��
��ʱ![]() ����FE=
����FE=![]() ��
��
![]() ����
����![]()
��![]() �����=
�����=![]() .
.
(3)������������ۣ�
������ͼ����G����AD���˶�ʱ������FG����G����GH��BC����BC�ཻ��H.
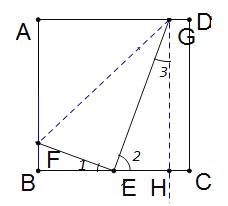
���GHE=90����
���2+��3=90����
��![]() ��
��
���1+��2=90����
���1=��3��
�ߡ�B=��GHE=90����
��Rt��BEF��Rt��HGE
��![]() ,
,
��BF=a����EH=2a
��EH��EC=20
��0��x��10
![]()
��ʱ����a=10ʱ��ȡ�����ֵ![]() .��a=0ʱ��ȡ����Сֵ
.��a=0ʱ��ȡ����Сֵ![]() .
.
������ͼ��![]() ʱ��G��CD��ʱ������FG��FG�е�OΪԲ����OFΪ�뾶��Բ��
ʱ��G��CD��ʱ������FG��FG�е�OΪԲ����OFΪ�뾶��Բ��
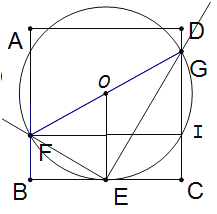
�ߡ�FEG=90����
��E���ڡ�O��
��BF=a��CG=b��
��EΪBC�е㣬FO=OG
��![]() ��
��
��FG=2OF=a+b
![]()
��FG//BCʱ����O�İ뾶��С����a+b��С��ʱa+b=FG=BC=40��![]() ��
��
���ͬ����֤Rt��BEF��Rt��CGE
��![]() ,��
,��![]()
��![]() ��a��b�ɷ�����������ϵ��
��a��b�ɷ�����������ϵ��
��O��DC�ཻ��I������FI��
���FIG=90��
�ߡ�B=��C=90��
���ı���BCIFΪ���Σ�
��IC=BF=a��GI=GC-IC=b-a
��Rt��FIG�У����ݹ��ɶ���
![]() ,��
,��![]()
�൱|b-a|���ʱa+b��ֵ���
��![]()
�൱a=10��b=40��a+b=50��
��a=40ʱ��b=10��a+b=50����ʱ![]() ������Ϊ500.
������Ϊ500.
�ۺϢ٢ڣ�![]() ��������ֵΪ500����СֵΪ400.
��������ֵΪ500����СֵΪ400.

 ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�