��Ŀ����
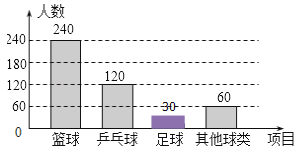
����Ŀ��ijѧ������Ϊ�˽ⱾУѧ��ϲ�������˶�������������ȡ��������ѧ�������ʾ����飬Ҫ��ÿλѧ��ֻ����дһ���Լ�ϲ���������˶�����������Ľ�����Ƴ����µ�������������ͳ��ͼ��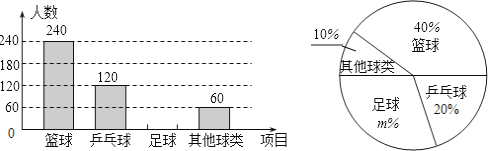
�����ͳ��ͼ���ṩ����Ϣ������������⣺
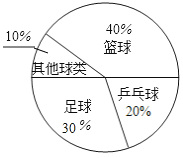
��1���μӵ���������������ˣ�������ͼ�У�m=����������ͼ����������
��2�������У��3500��ѧ���������ϲ��������ѧ�����ж����ˣ�
��3�������żƻ������������ƹ�����У������ȡ����������֯������������״ͼ���б��������ȡ������������ǡ���ǡ����͡����ĸ��ʣ�
���𰸡�
��1��
600��30����ͼ
��2��
�⣺3500��40%=1400���ˣ�
��ϲ��������ѧ������1400��
��3��
�⣺
���� | ���� | ƹ���� | |
���� | / | �������� | ����ƹ���� |
���� | �������� | / | ����ƹ���� |
ƹ���� | ƹ�������� | ƹ�������� | / |
2��6= ![]() ��
��
�𣺳�ȡ������������ǡ���ǡ����͡����ĸ����� ![]()
���������⣺��1����240��40%=600���ˣ�
��μӵ������������600�ˣ�
��1��40%��20%��10%=30%��
��������ͼ�У�m=30��
 .
.
�ʴ�Ϊ��600��30��
��1�����ȸ�������ͳ��ͼ������ͳ��ͼ����ϲ�����������������ռ�μӵ���������İٷ��ʣ�����μӵ�����������ж����ˣ�Ȼ��������ͼ�У���1��ȥϲ������ƹ��������������ѧ��ռ�İٷ��ʣ����m��ֵ�Ƕ��٣���������ͼ�����������ɣ���2���������⣬�ø�Уѧ����������ϲ��������ѧ��ռ�İٷ��ʣ����ϲ��������ѧ�����ж����˼��ɣ���3��Ӧ���б����������ȡ������������ǡ���ǡ����͡������������Լ�һ���ж����ֿ��ܣ������ȡ������������ǡ���ǡ����͡����ĸ����Ƕ��ټ��ɣ���1��������Ҫ�������б�������״ͼ����Ӧ�ã�Ҫ�������գ�������Ĺؼ���Ҫ��ȷ���б���Ŀ�����ڲ��ز�©���оٳ����п��ܵĽ�����n���ٴ���ѡ�������¼�A��B�Ľ����Ŀm��������ʣ���2�������������������������ķ�����Ӧ�ã�Ҫ�������գ�������Ĺؼ���Ҫ��ȷ��һ����˵��������ȥ��������ʱ������Խ���д����ԡ�����Խ����ʱ������Ĺ���Ҳ��Խ��ȷ����3���������������ͳ��ͼ������ͳ��ͼ�������˴�ͳ��ͼ�л�ȡ��Ϣ��������

����Ŀ��ij�߲˾�Ӫ�����߲������г������߲˽������ۣ������߲������۸������ۼ۸����:
�߲�Ʒ�� | ������ | �ཷ | ������ | ���� |
������(Ԫ/kg) | 3.6 | 5.4 | 8 | 4.8 |
���ۼ�(Ԫ/��) | 5.4 | 8.4 | 14 | 7.6 |
������������:
(1)��һ�죬�þ�Ӫ�������������������������߲˹�300 kg����ȥ��1520ԪǮ���������߲˵���ȫ������һ��������ԪǮ?
(2)�ڶ��죬�þ�Ӫ����1520ԪǮ��Ȼ��������������������Ҫ�뵱��ȫ�������Ǯ��1050Ԫ����þ�Ӫ����������������ǧ��?