题目内容
【题目】如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.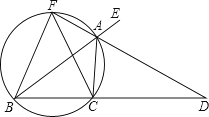
(1)求证:∠FBC=∠FCB;
(2)已知FAFD=12,若AB是△ABC外接圆的直径,FA=2,求CD的长.
【答案】
(1)
证明:∵四边形AFBC内接于圆,
∴∠FBC+∠FAC=180°,
∵∠CAD+∠FAC=180°,
∴∠FBC=∠CAD,
∵AD是△ABC的外角∠EAC的平分线,
∴∠EAD=∠CAD,
∵∠EAD=∠FAB,
∴∠FAB=∠CAD,
又∵∠FAB=∠FCB,
∴∠FBC=∠FCB;
(2)
解:由(1)得:∠FBC=∠FCB,
又∵∠FCB=∠FAB,
∴∠FAB=∠FBC,
∵∠BFA=∠BFD,
∴△AFB∽△BFD,
∴ ![]() ,
,
∴BF2=FAFD=12,
∴BF=2 ![]() ,
,
∵FA=2,
∴FD=6,AD=4,
∵AB为圆的直径,
∴∠BFA=∠BCA=90°,
∴tan∠FBA= ![]() =
= ![]() =
= ![]() ,
,
∴∠FBA=30°,
又∵∠FDB=∠FBA=30°,
∴CD=ADcos30°=4× ![]() =2
=2 ![]() .
.
【解析】(1)由圆内接四边形的性质和邻补角关系证出∠FBC=∠CAD,再由角平分线和对顶角相等得出∠FAB=∠CAD,由圆周角定理得出∠FAB=∠FCB,即可得出结论;
(2)由(1)得:∠FBC=∠FCB,由圆周角定理得出∠FAB=∠FBC,由公共角∠BFA=∠BFD,证出△AFB∽△BFD,得出对应边成比例求出BF,得出FD、AD的长,由圆周角定理得出∠BFA=∠BCA=90°,由三角函数求出∠FBA=30°,再由三角函数求出CD的长即可.本题考查了相似三角形的判定与性质、圆周角定理、圆内接四边形的性质、三角函数等知识;本题综合性强,有一定难度,证明三角形相似是解决问题的关键.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案