题目内容
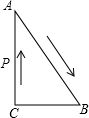 (2012•衢州模拟)如图,Rt△ABC中,∠C=90°,BC=3,AC=4,点P从点C出发沿C-A-B方向运动到点B,运动速度为1个单位每秒,运动时间为t,当△BCP为等腰三角形时,则t的值为
(2012•衢州模拟)如图,Rt△ABC中,∠C=90°,BC=3,AC=4,点P从点C出发沿C-A-B方向运动到点B,运动速度为1个单位每秒,运动时间为t,当△BCP为等腰三角形时,则t的值为3或6或
或
| 27 |
| 5 |
| 13 |
| 2 |
3或6或
或
.| 27 |
| 5 |
| 13 |
| 2 |
分析:当△BCP为等腰三角形时应分当C是顶角顶点,当B是顶角顶点,当P是顶角的顶点三种情况进行讨论,利用勾股定理和三角形的中位线定理求得BP的长,从而求解.
解答: 解:当C是顶角顶点时,当如图(1)所示:PC=BC=3,则运动的时间是3秒;
解:当C是顶角顶点时,当如图(1)所示:PC=BC=3,则运动的时间是3秒;
当如图(2)所示:CE=
=
=
,
在直角△BCE中,BE=
=
.
则PB=2BE=
,AC+AP=4+5-
=
;
当B是顶角顶点时,AP+AC=AC+AB-BP=4+5-3=6,则t的值是6;
当P是顶角的顶点时,P是BC的中垂线与AB的交点,如图(3),
 PE是△ABC的中位线,则PE=
PE是△ABC的中位线,则PE=
AC=2,
则直角△BPE中,BP=
=
=
,
则AC+AP=AC+AB-BP=4+5-
=
,则运动的时间t是
秒.
故答案是:3或6或
或
.
 解:当C是顶角顶点时,当如图(1)所示:PC=BC=3,则运动的时间是3秒;
解:当C是顶角顶点时,当如图(1)所示:PC=BC=3,则运动的时间是3秒;当如图(2)所示:CE=
| AC•BC |
| AB |
| 3×4 |
| 5 |
| 12 |
| 5 |
在直角△BCE中,BE=
| BC2-CE2 |
| 9 |
| 5 |
则PB=2BE=
| 18 |
| 5 |
| 18 |
| 5 |
| 27 |
| 5 |
当B是顶角顶点时,AP+AC=AC+AB-BP=4+5-3=6,则t的值是6;
当P是顶角的顶点时,P是BC的中垂线与AB的交点,如图(3),
 PE是△ABC的中位线,则PE=
PE是△ABC的中位线,则PE=| 1 |
| 2 |
则直角△BPE中,BP=
| BE2+PE2 |
22+(
|
| 5 |
| 2 |
则AC+AP=AC+AB-BP=4+5-
| 5 |
| 2 |
| 13 |
| 2 |
| 13 |
| 2 |
故答案是:3或6或
| 27 |
| 5 |
| 13 |
| 2 |
点评:本题考查了等腰三角形的性质,正确进行讨论是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
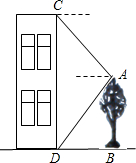 (2012•衢州模拟)小明为测量门前大树AB的高度,他先从房屋底部D处看树顶A的仰角为60°,之后小明爬上房屋顶部C处看树顶A的俯角为30°,已知小明家的房屋高度为8米,小明的身高忽略不计,求大树AB的高度.
(2012•衢州模拟)小明为测量门前大树AB的高度,他先从房屋底部D处看树顶A的仰角为60°,之后小明爬上房屋顶部C处看树顶A的俯角为30°,已知小明家的房屋高度为8米,小明的身高忽略不计,求大树AB的高度.