题目内容
【题目】如图,直线AB、CD、EF相交于点O . 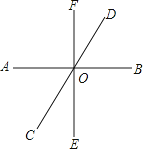
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
【答案】
(1)
【解答】∠COE的邻补角为∠COF和∠EOD
(2)
【解答】∠COE和∠BOE的对顶角分别为∠DOF和∠AOF
(3)
【解答】∵∠BOF=90°,
∴AB⊥EF
∴∠AOF=90°,
又∵∠AOC=∠BOD=60°
∴∠FOC=∠AOF+∠AOC=90°+60°=150°.
【解析】(1)根据邻补角的概念即可解答;(2)根据对顶角的概念即可解答;(3)因为∠BOF=90°,所以AB⊥EF , 由此可得∠AOF , 再根据对顶角的概念可得∠FOC的度数.
【考点精析】解答此题的关键在于理解对顶角和邻补角的相关知识,掌握两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目