题目内容
【题目】如图Ⅰ,已知:AD=AB,AD⊥AB,AC=AE,AC⊥AE.

(1)若反向延长△ABC的高AM交DE于点N,过D作DH⊥MN.求证:①DH=AM;②DN=EN
(2)如图Ⅱ,若AM为△ABC的中线,反向延长AM交DE于点N,求证:AN⊥DE.
【答案】(1)①见解析;②见解析;(2)见解析.
【解析】
(1)①利用AAS证明△ADH≌△BAM,可推出DH=AM;
②作EF⊥MN交MN的延长线于F,同法可证EF=AM,推出DH=EF,然后利用AAS证明△DNH≌△ENF即可;
(2)延长AM到F,使得MF=AM,证明四边形ABCF是平行四边形,再证明△ADE≌△CFA,得到∠E=∠CAF,由∠CAF+∠EAN=90°,推出∠EAN+∠E=90°,得到∠ANE=90°,即可求解.
(1)证明:①∵∠BAD=∠AHD=∠AMB=90°,
∴∠DAH+∠BAM=90°,∠DAH+∠ADH=90°,
∴∠BAM=∠ADH,
∵AB=AD,
∴△ADH≌△BAM(AAS),
∴DH=AM;
②如图,作EF⊥MN交MN的延长线于F,
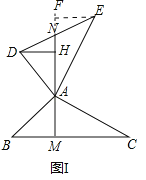
同①可证EF=AM,
∵DH=AM,
∴DH=EF,
∵∠DHN=∠EFN,∠DNH=∠ENF,
∴△DNH≌△ENF(AAS),
∴DN=EN;
(2)如图,延长AM到F,使得MF=AM,
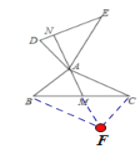
∵AM=MF,BM=CM,
∴四边形ABFC是平行四边形,
∴AB=CF,AB∥CF,
∴∠BAC+∠ACF=180°,
∵AD⊥AB, AC⊥AE
∴∠BAD=∠EAC=180°,
∴∠BAC+∠DAE=180°,
∴∠DAE=∠ACF,
∵AD=CF,AE=AC,
∴△ADE≌△CFA,
∴∠E=∠CAF,
∵∠CAF+∠EAN=90°,
∴∠EAN+∠E=90°,
∴∠ANE=90°,
∴AN⊥DE.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目






