题目内容
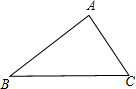
如图，在△ABC中，∠BAC=4∠ABC=4∠C，BD⊥AC，垂足为D，求∠ABD的度数．
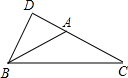
∵∠BAC=4∠ABC=4∠C（已知），
∴∠BAC+∠ABC+∠C=180°，
即∠C=∠ABC=180×
=30°（等式性质），
∴∠DAB=∠C+∠ABC=30°+30°=60°（外加性质），
∵BD⊥AC（已知），
∴∠BDA=90°（垂直定义），
则∠ABD=90°-60°=30°．
∴∠BAC+∠ABC+∠C=180°，
即∠C=∠ABC=180×
| 1 |
| 6 |
∴∠DAB=∠C+∠ABC=30°+30°=60°（外加性质），
∵BD⊥AC（已知），
∴∠BDA=90°（垂直定义），
则∠ABD=90°-60°=30°．
练习册系列答案
相关题目
