题目内容
如图,在直角梯形ABCD中,AB=2,BC=4,AD=6,M是CD的中点,点P在直角梯形的边上沿A→B→C→M运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示是
A. | B. | C. | D. |
D
解析试题分析:应用特殊元素法和排他法进行分析:
当点P运动到点B时,如图1,
作AB边上的高MH,
∵AB=2,BC=4,AD=6,M是CD的中点,
∴MH是梯形的中位线。∴MH= 。
。
∴△APM的面积=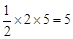 。
。
∴当x=2时,y=5。从而可排除A,B选项。
当点P运动到点C时,如图2,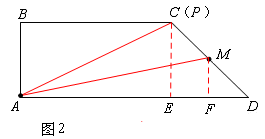
分别作△ACD和△AMD的AD边H的高CE和MF,
∵AB=2,BC=4,AD=6,M是CD的中点,
∴MF是△CDE的中位线。∴MF=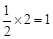 。
。
∴△APM的面积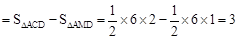 。
。
∴当x=6时,y=3。从而可排除C选项。
故选D。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,一次函数y=(m﹣2)x﹣1的图象经过二、三、四象限,则m的取值范围是( )
| A.m>0&nbs, | B.m<0&nbs, | C.m>2&nbs, | D.m<2&nbs, |
若点(-4,y1),(2,y2)都在直线y=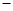 3x+t上,则y1与y2的大小关系是 ( )
3x+t上,则y1与y2的大小关系是 ( )
| A.y1>y2 | B.y1=y2 | C.y1<y2 | D.无法确定 |
体育课上,20人一组进行足球比赛,每人射点球5次,已知某一组的进球总数为49个,进球情况记录如下表,其中进2个球的有x人,进3个球的有y人,若(x,y)恰好是两条直线的交点坐标,则这两条直线的解析式是
| 进球数 | 0 | 1 | 2 | 3 | 4 | 5 |
| 人数 | 1 | 5 | x | y | 3 | 2 |

B.y=﹣x+9与

C.y=﹣x+9与

D.y=x+9与

某棵果树前x年的总产量y与x之间的关系如图所示,从目前记录的结果看,前x年的年平均产量最高,则x的值为【 】
| A.3 | B.5 | C.7 | D.9 |


 图像向下平移
图像向下平移 个单位,与双曲线
个单位,与双曲线 交于点A,与
交于点A,与 轴交于点B,则
轴交于点B,则 =( )
=( )


