题目内容
一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;……如此进行下去,直至得C13.若P(37,m)在第13段抛物线C13上,则m =_________.
2.
解析试题分析:把y=0代入y=-x(x-3),计算出点A1的坐标,通过分析可以知道将C1到C3相当于把C1的图象向右平移了2个0A1的距离,从而计算出从C1到C13向右平移的距离,然后根据点的的平移法则,求出在C13图象上点P的横坐标在C1图象上相应的横坐标,把相应的横坐标代入y=-x(x-3)中计算出纵坐标,根据纵坐标不变,即可求出m的值.
把把y=0代入y=-x(x-3),得:-x(x-3)=0,解之得:x1=0,x2=3,
∴点A1的坐标为(3,0)
∴OA1=3,
∴从图象C1到图象C3向右平移了6个单位,
∴从图象C1到图象C13向右平移了36个单位,
设点P在C1图象上对应的点为P1,
∴点P1的坐标为(1,m),
把x=1代入y=-x(x-3)中,得:y=-1×(1-3)=2,
∴m=2.
故填2.
考点:1二次函数图象的平移,2点的平移法则,3规律题.

练习册系列答案
相关题目
 中,直线
中,直线 和抛物线
和抛物线 在第一象限交于点A,过A作
在第一象限交于点A,过A作 轴于点
轴于点 .如果
.如果 取1,2,3,…,n时对应的△
取1,2,3,…,n时对应的△ 的面积为
的面积为
 ,那么
,那么 _____;
_____; _____.
_____.


 的最小值是 .
的最小值是 . 的图象如图所示,则下列结论中:①
的图象如图所示,则下列结论中:①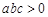 ;②
;② ;③
;③ ;④
;④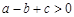 .正确的是 .
.正确的是 .
 与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为 .
与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为 .