如图.已知建筑物AB高21米.从另一建筑物CD的顶端C处测得AB的顶部A点的仰角为45°.又测得建筑物AB离地面1米的一阳台E处点的仰角为30°.求建筑物CD的高．(3≈1.73.结果精确到0.1米) 题目和参考答案——青夏教育精英家教网—

题目内容

如图，已知建筑物AB高21米，从另一建筑物CD的顶端C处测得AB的顶部A点的仰角为45°，又测得建筑物AB离地面1米的一阳台E处点的仰角为30°，求建筑物CD的高．（

≈1.73，结果精确到0.1米）

分析：设CD=x，则AF=21-x，EF=x-1，在Rt△CEF、Rt△ACF中分别表示出CF，建立方程即可解出x的值．

解答：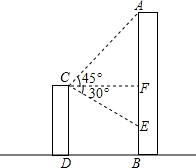

解：设CD=x，则AF=21-x，EF=x-1，
在Rt△CEF中，∠ECF=30°，
∵tan∠ECF=

，
∴CF=

（x-1），
在Rt△ACF中，∠ACF=45°，
∴CF=AF=21-x，
∴21-x=

（x-1），
解得：x≈8.3．
答：建筑物CD的高为8.3米．

点评：本题考查了解直角三角形的应用，解答本题的关键是构造直角三角形，利用锐角三角函数的定义表示出有关线段的长度．

练习册系列答案

≈1.732）．
（1）若修建的斜坡BE的坡角（即∠BEF）不大于45°，则平台DE的长最多为

11.0

米；
（2）一座建筑物GH距离坡角A点27米远（即AG=27米），小明在D点测得建筑物顶部H的仰角（即∠HDM）为30°．点B、C、A、G、H在同一个平面内，点C、A、G在同一条直线上，且HG⊥CG，问建筑物GH高为多少米？

如图，已知斜坡AB长60米，坡角（即∠BAC）为30°，BC⊥AC，现计划在斜坡中点D处挖去部分坡体（用阴影表示）修建一个平行于水平线CA的平台DE和一条新的斜坡BE．（下面两小题的结果都精确到0.1米，参考数据：

≈1.732）
（1）若修建的斜坡BE的坡度为1：0.8，则平台DE的长为

14.0

米；
（2）斜坡前的池塘内有一座建筑物GH，小明在平台E处测得建筑物顶部H的仰角（即∠HEM）为30°，测得建筑物顶部H在池塘中倒影H′的俯角为45°（即∠H′EM），测得点B、C、A、G、H、H′在同一个平面内，点C、A、G在同一条直线上，且HG⊥CG，求建筑物GH的高和AG的长．

如图，已知斜坡AB长60米，坡角（即∠BAC）为30°，BC⊥AC，现计划在斜坡中点D处挖去部分坡体（用阴影表示）修建一个平行于水平线CA的平台DE和一条新的斜坡BE.（请将下面2小题的结果都精确到0.1米，参考数据）.
【小题1】若修建的斜坡BE的坡角(即∠BAC)不大于45°,则平台DE的长最多为 ▲ 米；
【小题2】一座建筑物GH距离坡脚A点27米远（即AG=27米），小明在D点测得建筑物顶部H的仰角(即∠HDM)为30°.点B、C、A、G、H在同一个平面上，点C、A、G在同一条直线上，且HG⊥CG，问建筑物GH高为多少米？

如图，已知斜坡AB长60米，坡角（即∠BAC）为30°，BC⊥AC，现计划在斜坡中点D处挖去部分坡体（用阴影表示）修建一个平行于水平线CA的平台DE和一条新的斜坡BE．

（1）若修建的斜坡BE的坡角（即∠BEF）不大于45°，则平台DE的长最多为多少米？

（2）一座建筑物GH距离坡角A点27米远（即AG=27米），小明在D点测得建筑物顶部H的仰角（即∠DHM）为30°，点B、C、A、G、H在同一个平面内，点C、A、G在同一条直线上，且HG⊥CG，问建筑物GH高为多少米？

试题分类