Question

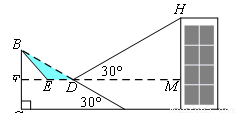
如图，已知斜坡AB长60米，坡角（即∠BAC）为30°，BC⊥AC，现计划在斜坡中点D处挖去部分坡体（用阴影表示）修建一个平行于水平线CA的平台DE和一条新的斜坡BE．

（1）若修建的斜坡BE的坡角（即∠BEF）不大于45°，则平台DE的长最多为多少米？

（2）一座建筑物GH距离坡角A点27米远（即AG=27米），小明在D点测得建筑物顶部H的仰角（即∠DHM）为30°，点B、C、A、G、H在同一个平面内，点C、A、G在同一条直线上，且HG⊥CG，问建筑物GH高为多少米？

 

Answer 1

【答案】

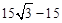（1）；（2）.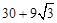

【解析】

试题分析：（1）根据题意得出，∠BEF最大为45°，当∠BEF=45°时，EF最短，此时ED最长，从而得出EF的长，即可得出答案；

（2）利用在Rt△DPA中，DP=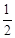AD，以及PA=AD•cos30°，从而得出DM的长，利用HM=DM•tan30°得出即可.

试题解析：（1）∵修建的斜坡BE的坡角（即∠BEF）不大于45°，∴∠BEF最大为45°.

当∠BEF=45°时，EF最短，此时ED最长.

∵∠DAC=∠BDF=30°，AD=BD=30，∴BF=EF=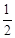BD=15，DF=.

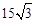∴DE=DF－EF=.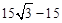

∴平台DE的长最多为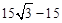米.

（2）如图，过点D作DP⊥AC，垂足为P.

在Rt△DPA中，DP=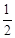AD=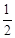×30=15，PA=AD•cos30°= 30×.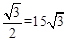

在矩形DPGM中，MG=DP=15，DM=PG=PA＋AG=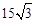+27。

在Rt△DMH中，HM=DM•tan30°=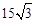（+27）×，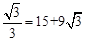

∴GH=HM＋MG=15+.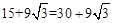

答：建筑物GH高为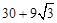米.

考点：1.解直角三角形的应用（坡度坡角问题）；2.锐角三角函数定义；3.特殊角的三角函数值.