Question

【题目】已知矩形ABCD中，对角线AC、BD相交于点O，AE⊥BD，垂足为E，AD=8,

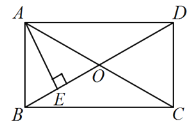
(1)若∠DAE︰∠BAE=3︰1，求∠EAC的度数；

(2)若ED=3BE，求AE的长．

Answer 1

【答案】（1）45°；（2）4.

【解析】

（1）由已知条件求出∠BAE＝22.5°，再根据矩形的性质得到OA＝OB，求出∠OAB=∠ABE=67.5°，即可得出∠EAC的度数；

（2）根据矩形的性质和等腰三角形三线合一的性质得到△OAB是等边三角形，求出∠ADE =30°，利用含30°角的直角三角形的性质可求出AE.

(1)解：∵∠DAE︰∠BAE=3︰1，

∴∠BAE=90°×=22.5°，

∴∠ABE=67.5°，

∵四边形ABCD是矩形，

∴AC=BD，AO=CO，BO=DO

∴OA=OB，

∴∠OAB=∠ABE=67.5°

∴∠EAC=∠OAB∠BAE=67.5°22.5°=45°；

(2)∵OA=OB=OD，ED=3BE，

∴OE+OD=3BE，

∴OBBE+OB=3BE，

∴OB =2BE，

∴点E为OB的中点，

∵AE⊥BD，

∴AB=OA，

∴OA=AB=OB，即△OAB是等边三角形，

∴∠ABD=60°，

∴∠ADE=90°∠ABD=30°，

∵AE⊥BD，AD=8，

∴AE=AD=4.