题目内容
 如图,平行四边形ABCD中,AE是BC边上的高,AE是BC沿BC方向平移,使点E与点C重合,得△GFC.
如图,平行四边形ABCD中,AE是BC边上的高,AE是BC沿BC方向平移,使点E与点C重合,得△GFC.
(1)求证:BE=DG:
(2)若四边形ABFG是菱形,且AB:BC=2:3,求∠B的度数.
解:(1)∵∠ABE=∠CDG,∠AEB=∠CGD,AE=CG,
∴△ABE≌△CDG,
∴BE=DG,
(2)四边形ABFG是菱形,则BF=AB,
∵AB:BC=2:3
∴FC= AB,
AB,
∵AE是BC沿BC方向平移,使点E与点C重合,得△GFC.
∴BE=FC,
∴AB=2BE,
∴直角△ABE中,∠BAE=30°,
∴∠ABE=60°.
分析:(1)求证△ABE≌△CDG,根据全等三角形对应边相等的性质可得BE=DG;
( 2)根据BF=AB,AB:BC=2:3,BE=FC,即可求得AB=2BE,即可求得直角△ABE中,∠BAE=30°,故可求得∠ABE=60°.
点评:本题考查了菱形各边长相等的性质,考查了全等三角形的证明和全等三角形对应边相等的性质,考查了含30°角的直角三角形的应用,本题中求证AB=2BE是解题的关键.
∴△ABE≌△CDG,
∴BE=DG,
(2)四边形ABFG是菱形,则BF=AB,
∵AB:BC=2:3
∴FC=
 AB,
AB,∵AE是BC沿BC方向平移,使点E与点C重合,得△GFC.
∴BE=FC,
∴AB=2BE,
∴直角△ABE中,∠BAE=30°,
∴∠ABE=60°.
分析:(1)求证△ABE≌△CDG,根据全等三角形对应边相等的性质可得BE=DG;
( 2)根据BF=AB,AB:BC=2:3,BE=FC,即可求得AB=2BE,即可求得直角△ABE中,∠BAE=30°,故可求得∠ABE=60°.
点评:本题考查了菱形各边长相等的性质,考查了全等三角形的证明和全等三角形对应边相等的性质,考查了含30°角的直角三角形的应用,本题中求证AB=2BE是解题的关键.

练习册系列答案
相关题目
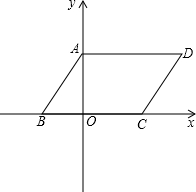 次方程x2-7x+12=0的两个根,且OA>OB.
次方程x2-7x+12=0的两个根,且OA>OB.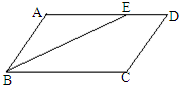 10、如图,平行四边形ABCD中,∠ABC的角平分线BE交AD于E点,AB=3,ED=1,则平行四边形ABCD的周长是
10、如图,平行四边形ABCD中,∠ABC的角平分线BE交AD于E点,AB=3,ED=1,则平行四边形ABCD的周长是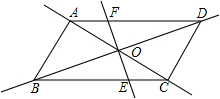
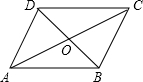 如图,平行四边形ABCD中,对角线AC和BD相交于点O,如果AC=12,BD=10,AB=m,那么m的取值范围是
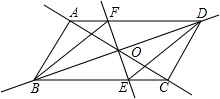
如图,平行四边形ABCD中,对角线AC和BD相交于点O,如果AC=12,BD=10,AB=m,那么m的取值范围是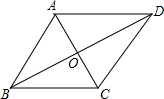 如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,DB=8,则四边形ABCD是的周长为
如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,DB=8,则四边形ABCD是的周长为