题目内容
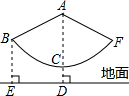 (2012•曲阜市模拟)如图,秋千拉绳长AB为3米,静止时踩板离地面0.5米,小朋友荡该秋千时,秋千在最高处时踩板离地面2米(左右对称),请计算该秋千所荡过的圆弧BF长是( )
(2012•曲阜市模拟)如图,秋千拉绳长AB为3米,静止时踩板离地面0.5米,小朋友荡该秋千时,秋千在最高处时踩板离地面2米(左右对称),请计算该秋千所荡过的圆弧BF长是( )分析:根据题意先作辅助线BG⊥AC于G,然后确定AG=1.5m,根据在直角三角形中,一条直角边等于斜边的一半,得∠BAG=60°,从而求得∠BAF=120°,最后求出弧长.
解答:解:
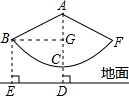
由题意得,BE=2m,AC=3m,CD=0.5m,
作BG⊥AC于G,则AG=AD-GD=AC+CD-BE=1.5m,
由于AB=3,所以在Rt△ABG中,∠BAG=60°,
根据对称性,知∠BAF=120°,
故秋千所荡过的圆弧长是
=2π(米),
故选B.

由题意得,BE=2m,AC=3m,CD=0.5m,
作BG⊥AC于G,则AG=AD-GD=AC+CD-BE=1.5m,
由于AB=3,所以在Rt△ABG中,∠BAG=60°,
根据对称性,知∠BAF=120°,
故秋千所荡过的圆弧长是
| 120π×3 |
| 180 |
故选B.
点评:本题考查了弧长的计算,属于基础题,解答本题的关键是熟练掌握弧长的计算公式,难度一般.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
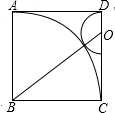 (2012•曲阜市模拟)如图,在正方形ABCD中,O是CD边上一点,以O为圆心,OD为半径的半圆恰好与以B为圆心,BC为半径的扇形的弧外切,则sin∠OBC的值为( )
(2012•曲阜市模拟)如图,在正方形ABCD中,O是CD边上一点,以O为圆心,OD为半径的半圆恰好与以B为圆心,BC为半径的扇形的弧外切,则sin∠OBC的值为( )