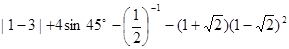题目内容
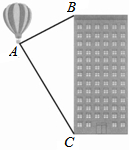
我国为了维护队钓鱼岛P的主权,决定对钓鱼岛进行常态化的立体巡航.在一次巡航中,轮船和飞机的航向相同(AP∥BD),当轮船航行到距钓鱼岛20km的A处时,飞机在B处测得轮船的俯角是45°;当轮船航行到C处时,飞机在轮船正上方的E处,此时EC=5km.轮船到达钓鱼岛P时,测得D处的飞机的仰角为30°.试求飞机的飞行距离BD(结果保留根号).


解:作AF⊥BD,PG⊥BD,垂足分别为F、G,

由题意得:AF=PG=CE=5km,FG=AP=20km,
在Rt△AFB中,∠B=45°,则∠BAF=45°。
∴BF=AF=5。
∵AP∥BD,∴∠D=∠DPH=30°。
在Rt△PGD中, ,即
,即 。
。
∴GD=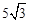 。
。
∴BD=BF+FG+DC=5+20+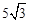 =25+
=25+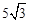 (km)。
(km)。
答:飞机的飞行距离BD为25+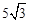 km。
km。

由题意得:AF=PG=CE=5km,FG=AP=20km,
在Rt△AFB中,∠B=45°,则∠BAF=45°。
∴BF=AF=5。
∵AP∥BD,∴∠D=∠DPH=30°。
在Rt△PGD中,
 ,即
,即 。
。∴GD=
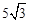 。
。∴BD=BF+FG+DC=5+20+
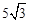 =25+
=25+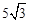 (km)。
(km)。答:飞机的飞行距离BD为25+
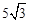 km。
km。作AF⊥BD,PG⊥BD,构造直角三角形,在Rt△ABF和△PDG中分别求出BF、GD的值,继而可求得BD=BF+FG+DC的值。

练习册系列答案
相关题目
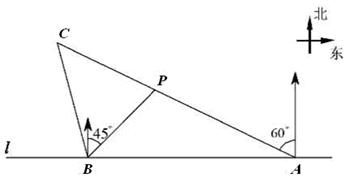
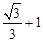
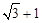
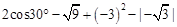 ,(说明:本题不能使用计算器)
,(说明:本题不能使用计算器) .
.
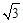 m
m 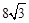 km的C处.
km的C处.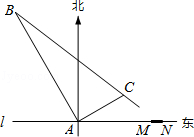
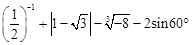 .
.