题目内容
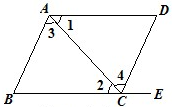
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交B于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.
A.1 B.2 C.3 D.4
D.
解析试题分析:①根据作图的过程可知,AD是∠BAC的平分线.故①正确;
②如图,∵在△ABC中,∠C=90°,∠B=30°,∴∠CAB=60°.
又∵AD是∠BAC的平分线,
∴∠1=∠2=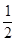 ∠CAB=30°,
∠CAB=30°,
∴∠3=90°-∠2=60°,即∠ADC=60°.故②正确;
③∵∠1=∠B=30°,∴AD=BD,∴点D在AB的中垂线上.故③正确;
④∵如图,在直角△ACD中,∠2=30°,∴CD=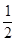 AD,
AD,
∴BC=CD+BD=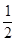 AD+AD=
AD+AD= AD,S△DAC=
AD,S△DAC=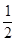 AC•CD=
AC•CD=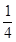 AC•AD.
AC•AD.
∴S△ABC=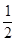 AC•BC=
AC•BC=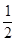 AC•
AC• AD=
AD= AC•AD,
AC•AD,
∴S△DAC:S△ABC=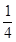 AC•AD:
AC•AD: AC•AD=1:3.故④正确.
AC•AD=1:3.故④正确.
综上所述,正确的结论是:①②③④,共有4个.
故选D.
考点: 1.角平分线的性质;2.线段垂直平分线的性质;3.作图—基本作图.

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案如图,把一块等腰直角三角板的直角顶点放在直尺的一边上,如果∠1=40°,那么∠2=( )
| A.40° | B.45° | C.50° | D.60° |
如图,△ABC中,∠A=90°,点D在AC边上,DE∥BC,如果∠1=145°,那么∠B的度数为( )
A.35° | B.25° | C.45° | D.55° |
如图,OD⊥AB于O,OC⊥OE,图中与∠AOC互补的角有
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,AB∥CD,CE平分∠BCD,∠DCE=18°,则∠B的度数为( )
| A.18° | B.36° | C.45° | D.54° |
在时刻8∶30时,时钟上的时针与分针间的夹角是
| A.75° | B.85° | C.70° | D.60° |
45°角的余角是( )
| A.30° | B.45° | C.60° | D.135° |
如果要在一条直线上得到6条不同的线段,那么在这条直线上应选几个不同的点( )
| A.3个 | B.4个 | C.5个 | D.6个 |