题目内容
如图①是一个八角星形纸板,是由正方形绕着它的中心顺时针旋转45°形成的,将纸板沿如图②的虚线进行切割,无缝隙无重叠地拼成图③所示的大正方形,其面积为16+8
,则图③中线段AB的长为
| 2 |
2+
| 2 |
2+
.| 2 |

分析:根据题中信息可得图2、图3面积相等;图2可分割为一个正方形和四个小三角形;设原八角形边长为a,则图2正方形边长为2a+
a、面积为(2a+
a)2,四个小三角形面积和为2a2,解得a=
,进而得出EF的长.
| 2 |
| 2 |
| 2 |
解答: 解:设原八角形边长为a,则图2正方形边长为2a+
解:设原八角形边长为a,则图2正方形边长为2a+
a、面积为(2a+
a)2,四个小三角形面积和为2a2,
列式得(2a+
a)2+2a2=16+8
,
解得:a=
,
由题意可得出:EF=
EC=
(2
+2)=4+2
,
则AB=
EF=2+
.
故答案为:2+
.
 解:设原八角形边长为a,则图2正方形边长为2a+
解:设原八角形边长为a,则图2正方形边长为2a+| 2 |
| 2 |
列式得(2a+
| 2 |
| 2 |
解得:a=
| 2 |
由题意可得出:EF=
| 2 |
| 2 |
| 2 |
| 2 |
则AB=
| 1 |
| 2 |
| 2 |
故答案为:2+
| 2 |
点评:此题主要考查了图形的剪拼,解此题的关键是抓住图3中的AB在图2中是哪两条线段组成的,再列出方程求出即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则图3中线段
,则图3中线段 的长为 .
的长为 . 
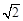 ,则图3中线段AB的长为_______.
,则图3中线段AB的长为_______.
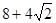 ,则图3中线段
,则图3中线段 的长为
.
的长为
. 
 ,则图3中线段AB的长为( )。
,则图3中线段AB的长为( )。