题目内容
图1是一个八角星形纸板,图中有八个直角,八个相等的钝角,每条边都相等.如图2将纸板沿虚线进行切割,无缝隙无重叠的拼成图3所示的大正方形,其面积为8+4| 2 |

分析:根据题中信息可得图2、图3面积相等;图2可分割为一个正方形和四个小三角形;设原八角形边长为a,则图2正方形边长为2a+
a、面积为(2a+
a)2,四个小三角形面积和为2a2,解得a=1.AB就知道等于多少了.
| 2 |
| 2 |
解答:解:设原八角形边长为a,则图2正方形边长为2a+
a、面积为(2a+
a)2,四个小三角形面积和为2a2,
列式得(2a+
a)2+2a2=8+4
,解得a=1,则AB=1+
.
| 2 |
| 2 |
列式得(2a+
| 2 |
| 2 |
| 2 |
点评:解此题的关键是抓住图3中的AB在图2中是哪两条线段组成的,再列出方程求出即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则图3中线段
,则图3中线段 的长为 .
的长为 . 
 ,则图3中线段
,则图3中线段 的长为 .
的长为 . 
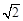 ,则图3中线段AB的长为_______.
,则图3中线段AB的长为_______.
 ,则图3中线段
,则图3中线段 的长为
.
的长为
. 