题目内容
如图，在数轴上，点A、B、C所对应的数分别为a、b、c，且OA=OB，则下列结论：①a、b、c一定都是有理数，②a+b=0，③a＜b＜c，④BC=|b-c|，其中正确的有（ ）
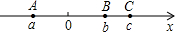
A．1个
B．2个
C．3个
D．4个
【答案】分析：根据数轴上的数与实数具有一一对应关系，以及数轴上的数左边的总数大于右边的数，即可作出判断．
解答：解：①数轴上的数表示实数，既可以是有理数，也可以是无理数，故结论错误；
②根据数轴可以得到：a，b异号，而OA=OB，则a，b胡为相反数，则a+b=0，则结论正确；
③根据数轴上的数：右边的总是大于左边的数，即可得到：a＜b＜c，故结论正确；
④正确．
则正确的是：②③④，故选C．
点评：本题考查了数轴与实数的关系，以及相反数的定义，引进了数轴，我们把数和点对应起来，也就是把“数”和“形”结合起来，二者互相补充，相辅相成，把很多复杂的问题转化为简单的问题，在学习中要注意培养数形结合的数学思想．
解答：解：①数轴上的数表示实数，既可以是有理数，也可以是无理数，故结论错误；
②根据数轴可以得到：a，b异号，而OA=OB，则a，b胡为相反数，则a+b=0，则结论正确；
③根据数轴上的数：右边的总是大于左边的数，即可得到：a＜b＜c，故结论正确；
④正确．
则正确的是：②③④，故选C．
点评：本题考查了数轴与实数的关系，以及相反数的定义，引进了数轴，我们把数和点对应起来，也就是把“数”和“形”结合起来，二者互相补充，相辅相成，把很多复杂的问题转化为简单的问题，在学习中要注意培养数形结合的数学思想．
练习册系列答案
阶梯计算系列答案
相关题目
19、如图，在数轴上与点A距离为3的点所表示的数是
原来的速度向相反的方向运动，设运动的时间为t（秒），