Question

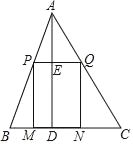
【题目】如图，在△ABC中，点PQ分别在AB，AC上，且PQ∥BC，PM⊥BC于点M，QN⊥BC于点N．AD⊥BC于点D，交PQ于点E，且AD＝BC．

（1）求AE：PQ的值；

（2）请探究BM，CN．QN之间的等量关系，并说明理由；

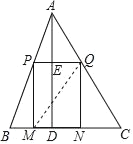
（3）连接MQ，若△ABC的面积等于8，求MQ的最小值．

Answer 1

【答案】（1）AE：PQ＝1；（2）QN＝BM+CN，理由见解析；（3）当x＝4时，MQ有最小值是4．

【解析】

（1）根据平行线的性质得到AE⊥PQ，根据相似三角形的性质得到，求得AE：PQ＝AD：BC，由于AD＝BC，于是得到结论；

（2）根据垂直的定义得到∠PMN＝∠MNQ＝∠MPQ＝90°，推出四边形PMNQ是矩形，得到PQ＝MN，PM＝ED，等量代换即可得到结论；

（3）根据三角形的面积得到12BCAD＝8，求得BC＝4，AD＝4，设MN＝x，则BM＋CN＝8x，PM＝QN＝8x，根据勾股定理即可得到结论．

（1）∵PQ∥BC，AD⊥BC，

∴AE⊥PQ，

∵PQ∥BC，

∴△APQ∽△ABC，

，

∴AE：PQ＝AD：BC，

∵AD＝BC，

∴AE：PQ＝AD：BC＝1；

（2）QN＝BM+CN，

理由是：∵PM⊥BC，QN⊥BC，

∴∠PMN＝∠MNQ＝∠MPQ＝90°，

∴四边形PMNQ是矩形，

∴PQ＝MN，PM＝ED，

∵AE＝PQ，AD＝BC，

∴AE+ED＝BM+MN+CN，

∴MN+QN＝BM+MN+CN，

∴QN＝BM+CN；

（3）∵△ABC的面积等于8，

∴BCAD＝8，

∵AD＝BC，

∴ BC2＝8，

∴BC＝4，AD＝4，

设MN＝x，则BM+CN＝8﹣x，PM＝QN＝8﹣x，

∵MQ＝,

∴当x＝4时，MQ有最小值是．