题目内容
在边长为1的等边三角形内任意放一些点,要使得至少存在2个点之间的距离不超过 ,那么至少应该放几个点
,那么至少应该放几个点
- A.n2+1
- B.2n+1
- C.2n
- D.n+1
A
分析:把三角形每条边分成n份,相应点之间连线,则可把三角形分成分成n2个边长为 的小三角形,则比三角形的个数多1可以保证至少有两个点落在同一小三角形内,即可解题.
的小三角形,则比三角形的个数多1可以保证至少有两个点落在同一小三角形内,即可解题.
解答:把三角形每条边分成n份,相应点之间连线,
可以把三角形分成n2个边长为 的小三角形,
的小三角形,
至少n2+1个点可以保证至少有两个点落在同一个小三角形内,
所以那两个点的距离是不超过 的.
的.
故选A.
点评:本题考查了等边三角形各边长相等的性质,学生探究发现规律的能力,本题中构建n2个三角形是解题的关键.
分析:把三角形每条边分成n份,相应点之间连线,则可把三角形分成分成n2个边长为
 的小三角形,则比三角形的个数多1可以保证至少有两个点落在同一小三角形内,即可解题.
的小三角形,则比三角形的个数多1可以保证至少有两个点落在同一小三角形内,即可解题.解答:把三角形每条边分成n份,相应点之间连线,
可以把三角形分成n2个边长为
 的小三角形,
的小三角形,至少n2+1个点可以保证至少有两个点落在同一个小三角形内,
所以那两个点的距离是不超过
 的.
的.故选A.
点评:本题考查了等边三角形各边长相等的性质,学生探究发现规律的能力,本题中构建n2个三角形是解题的关键.

练习册系列答案
相关题目
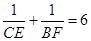 ,则等边三角
,则等边三角
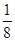 B.
B. 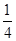 C.
C.
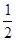 D.1
D.1