Question

【题目】如图，AB∥CD，分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系，请你从所得到的关系中任选一个加以说明。（适当添加辅助线，其实并不难）

(1) (2) (3) (4)

Answer 1

【答案】（1）∠APC=∠PAB+∠PCD；（2）∠APC+∠PAB+∠PCD =360°；（3）∠PAB=∠APC+∠PCD；（4）∠PCD=∠APC+∠PAB.

【解析】试题分析：关键过转折点作出平行线，根据两直线平行，内错角相等，或结合三角形的外角性质求证即可．

解：如图：

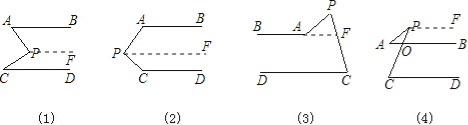
（1）∠APC=∠PAB+∠PCD；

证明：过点P作PF∥AB，则AB∥CD∥PF，

∴∠APC=∠PAB+∠PCD（两直线平行，内错角相等）．

（2）∠APC+∠PAB+∠PCD=360°；

（3）∠APC=∠PAB﹣∠PCD；

（4）∵AB∥CD，

∴∠POB=∠PCD，

∵∠POB是△AOP的外角，

∴∠APC+∠PAB=∠POB，

∴∠APC=∠POB﹣∠PAB，

∴∠APC=∠PCD﹣∠PAB．