题目内容
(2013•石峰区模拟)已知一元二次方程x2-2x+m=0
(1)若方程有两个实数根,求m的取值范围.
(2)若方程的两个实数根为x1,x2,且x1=-3x2,求m的值.
(1)若方程有两个实数根,求m的取值范围.
(2)若方程的两个实数根为x1,x2,且x1=-3x2,求m的值.
分析:(1)根据一元二次方程根的判别式的意义得到△=4-4m≥0,然后解不等式即可;
(2)根据一元二次方程的根与系数的关系得到x1+x2=2,x1•x2=m,由于x1=-3x2,则-3x2+x2=2,可先计算出解得x2,然后计算出x1,最后得到m的值.
(2)根据一元二次方程的根与系数的关系得到x1+x2=2,x1•x2=m,由于x1=-3x2,则-3x2+x2=2,可先计算出解得x2,然后计算出x1,最后得到m的值.
解答:解:(1)根据题意△=4-4m≥0,
解得m≤1;
(2)根据题意得为x1+x2=2,x1•x2=m,
∵x1=-3x2,
∴-3x2+x2=2,解得x2=-1,
∴x1=3,
∴m=-1×3=-3.
解得m≤1;
(2)根据题意得为x1+x2=2,x1•x2=m,
∵x1=-3x2,
∴-3x2+x2=2,解得x2=-1,
∴x1=3,
∴m=-1×3=-3.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的根与系数的关系.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
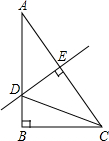 (2013•石峰区模拟)如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E为垂足,连接CD,若BD=1,则AC的长是
(2013•石峰区模拟)如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E为垂足,连接CD,若BD=1,则AC的长是 (2013•石峰区模拟)如图所示,在半径为5的⊙O中,弦AB=6,点C是优弧
(2013•石峰区模拟)如图所示,在半径为5的⊙O中,弦AB=6,点C是优弧
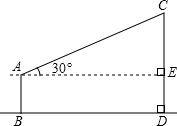 (2013•石峰区模拟)如图所示,小明测量学校旗杆的高度,他在离电线杆CD距离为15米的地方放置一个高1.5米的测角仪(AB),此时,经A处测得旗杆上顶端C处的仰角为30°.请问:这样就能够测出旗杆CD的高度吗?如果能,CD的高是多少米?(结果精确到0.1)
(2013•石峰区模拟)如图所示,小明测量学校旗杆的高度,他在离电线杆CD距离为15米的地方放置一个高1.5米的测角仪(AB),此时,经A处测得旗杆上顶端C处的仰角为30°.请问:这样就能够测出旗杆CD的高度吗?如果能,CD的高是多少米?(结果精确到0.1)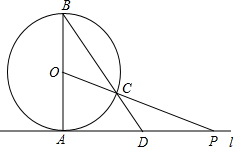 (2013•石峰区模拟)如图,已知直线L与⊙O相切于点A,直径AB=6,点P在L上移动,连结OP交⊙O于点C,连结BC并延长BC交直线l于点D.
(2013•石峰区模拟)如图,已知直线L与⊙O相切于点A,直径AB=6,点P在L上移动,连结OP交⊙O于点C,连结BC并延长BC交直线l于点D.