题目内容
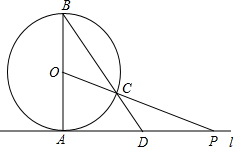 (2013•石峰区模拟)如图,已知直线L与⊙O相切于点A,直径AB=6,点P在L上移动,连结OP交⊙O于点C,连结BC并延长BC交直线l于点D.
(2013•石峰区模拟)如图,已知直线L与⊙O相切于点A,直径AB=6,点P在L上移动,连结OP交⊙O于点C,连结BC并延长BC交直线l于点D.(1)若AP=4,求线段PC的长;
(2)若△PAO与△BAD相似,求∠APO的度数.
(3)在(2)的条件下,试求四边形OADC的面积.(答案可保留根号)
分析:(1)求出AO、OC,根据勾股定理求出OP,即可求出答案;
(2)求出∠B=∠CPD=∠DCP=∠OCB,得出3∠B=90°,求出即可;
(3)连接AC,求出AC、BC,求出△ACB面积,即可求出△BOC面积,求出AD,求出△ABD面积,即可求出答案.
(2)求出∠B=∠CPD=∠DCP=∠OCB,得出3∠B=90°,求出即可;
(3)连接AC,求出AC、BC,求出△ACB面积,即可求出△BOC面积,求出AD,求出△ABD面积,即可求出答案.
解答:解:(1)∵PA切⊙O于A,
∴∠OAP=90°,
∵AB=6,
∴AO=OC=2,
在Rt△OAP中,AP=4,AO=3,由勾股定理得:OP=5,
∴PC=OP-OC=2;
(2)∵△PAO和△BAD相似,
∴∠B=∠CPD,
∵OB=OC,
∴∠B=∠OCB=∠DCP=∠CPD,
∴∠BDA=∠DCP+∠CPD=2∠B,
在Rt△BAD中,3∠B=90°,
∴∠B=30°,
∴∠APO=30°.
(3)∵△BAD中,∠BAD=90°,∠B=30°,AB=6,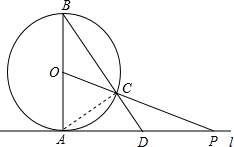
∴AD=AB•tan30°=2
,
∴△BAD面积是
AB×AD=
×6×2
=6
,
连接AC,
∵AB是直径,
∴∠ACB=90°,
∵AB=6,∠B=30°,
∴AC=3,BC=3
,
∴△ABC的面积是
AC×BC=
×3×3
=4.5
,
∵OB=OA,
∴△BOC的面积是
×4.5
=
S四边形OADC=S△BAD-S△BOC=
.
∴∠OAP=90°,
∵AB=6,
∴AO=OC=2,
在Rt△OAP中,AP=4,AO=3,由勾股定理得:OP=5,
∴PC=OP-OC=2;
(2)∵△PAO和△BAD相似,
∴∠B=∠CPD,
∵OB=OC,
∴∠B=∠OCB=∠DCP=∠CPD,
∴∠BDA=∠DCP+∠CPD=2∠B,
在Rt△BAD中,3∠B=90°,
∴∠B=30°,
∴∠APO=30°.
(3)∵△BAD中,∠BAD=90°,∠B=30°,AB=6,

∴AD=AB•tan30°=2
| 3 |
∴△BAD面积是
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
连接AC,
∵AB是直径,
∴∠ACB=90°,
∵AB=6,∠B=30°,
∴AC=3,BC=3
| 3 |
∴△ABC的面积是
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∵OB=OA,
∴△BOC的面积是
| 1 |
| 2 |
| 3 |
| 9 |
| 4 |
| 3 |
S四边形OADC=S△BAD-S△BOC=
| 15 |
| 4 |
| 3 |
点评:本题考查了含30度角的直角三角形性质,圆周角定理,勾股定理,三角形内角和定理的应用,主要考查学生的推理能力和计算能力,

练习册系列答案
相关题目
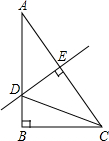 (2013•石峰区模拟)如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E为垂足,连接CD,若BD=1,则AC的长是
(2013•石峰区模拟)如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E为垂足,连接CD,若BD=1,则AC的长是 (2013•石峰区模拟)如图所示,在半径为5的⊙O中,弦AB=6,点C是优弧
(2013•石峰区模拟)如图所示,在半径为5的⊙O中,弦AB=6,点C是优弧
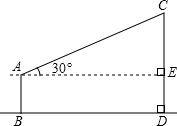 (2013•石峰区模拟)如图所示,小明测量学校旗杆的高度,他在离电线杆CD距离为15米的地方放置一个高1.5米的测角仪(AB),此时,经A处测得旗杆上顶端C处的仰角为30°.请问:这样就能够测出旗杆CD的高度吗?如果能,CD的高是多少米?(结果精确到0.1)
(2013•石峰区模拟)如图所示,小明测量学校旗杆的高度,他在离电线杆CD距离为15米的地方放置一个高1.5米的测角仪(AB),此时,经A处测得旗杆上顶端C处的仰角为30°.请问:这样就能够测出旗杆CD的高度吗?如果能,CD的高是多少米?(结果精确到0.1)