题目内容
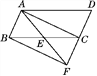
【题目】如图,已知点E是ABCD中BC边的中点,连接AE并延长交DC的延长线于点F.
(1)连接AC,BF,若∠AEC=2∠ABC,求证:四边形ABFC为矩形;
(2)在(1)的条件下,若△AFD是等边三角形,且边长为4,求四边形ABFC的面积.
【答案】(1)见解析;(2)4![]()
【解析】试题分析: ![]() 由
由![]() 为平行四边形,根据平行四边形的对边平行得到
为平行四边形,根据平行四边形的对边平行得到![]() 与
与![]() 平行,根据两直线平行内错角相等得到一对角相等,由
平行,根据两直线平行内错角相等得到一对角相等,由![]() 为
为![]() 的中点,得到两条线段相等,再由对应角相等,利用
的中点,得到两条线段相等,再由对应角相等,利用![]() 可得出
可得出![]() 进而得出
进而得出![]() 即可得出四边形
即可得出四边形![]() 是平行四边形,再判定对角线相等,即可得出平行四边形
是平行四边形,再判定对角线相等,即可得出平行四边形![]() 是矩形.
是矩形.
![]() 由等边三角形的性质得出
由等边三角形的性质得出![]() 得出
得出![]() 由矩形的性质得出
由矩形的性质得出![]() 得出
得出![]() 即可得出四边形
即可得出四边形![]() 的面积
的面积![]()
试题解析: ![]() ∵四边形
∵四边形![]() 为平行四边形,
为平行四边形,
![]()
![]()
又∵点![]() 为
为![]() 的中点,
的中点,
![]()
在![]() 和
和![]() 中,
中,
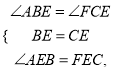
![]()
![]()
又![]()
∴四边形![]() 为平行四边形.
为平行四边形.
![]()
![]() 为
为![]() 的外角,
的外角,
![]()
又![]()
![]()
![]()
![]()
即![]()
∴四边形![]() 为矩形.
为矩形.
![]() 解:∵四边形
解:∵四边形![]() 是矩形,
是矩形,
![]()
又![]() 是等边三角形,
是等边三角形,
![]()
![]()
![]()

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目