题目内容
【题目】分解2x4﹣3x3+mx2+7x+n,其中含因式(x+2)和(x﹣1),求m,n.
【答案】解:∵分解2x4﹣3x3+mx2+7x+n,其中含因式(x+2)和(x﹣1),
∴x=1、x=﹣2肯定是关于x的方程2x4﹣3x2+mx2+7x+n=0的两个根,
∴![]() ,
,
解得: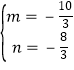 .
.
【解析】由“多项式2x4﹣3x3+mx2+7x+n含有因式(x﹣1)和(x+2)”得到“x=1、x=﹣2肯定是关于x的方程2x4﹣3x3+mx2+7x+n=0的两个根”,所以将其分别代入该方程列出关于m、n的方程组,通过解方程组来求m、n的值.
【考点精析】掌握解二元一次方程组和因式分解的定义是解答本题的根本,需要知道二元一次方程组:①代入消元法;②加减消元法;因式分解的最后结果必须是几个整式的乘积,否则不是因式分解;因式分解的结果必须进行到每个因式在有理数范围内不能再分解为止.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目

