Question

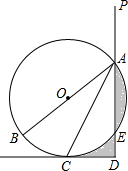如图，已知AB是⊙O的直径，AC是弦，且平分∠BAD，AD⊥CD，垂足为D，交⊙O于点E
（1）求证：CD是⊙O的切线；
（2）若CD=2，AD=，求⊙O的半径；
（3）在（2）的条件下，求图中阴影部分的面积．

Answer 1

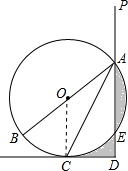（1）证明：连接OC．
∵OA=OC（⊙O的半径），
∴∠OCA=∠OAC（等边对等角）；
又∵AC平分∠BAD，
∴∠OAC=∠CAD，
∴∠ACO=∠CAD（等量代换），
∴OC∥AD（内错角相等，两直线平行）；
而AD⊥CD，
∴OC⊥CD，即CD是⊙O的切线；

（2）解：∵AD⊥CD，
∴在Rt△ADC中，
AC=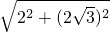=4，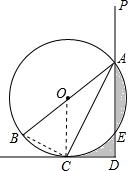
连接BC，则∠ACB=90°
∵∠DAC=∠OAC
∴△ADC∽△ACB
∴
∴AB===，
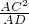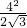∴OB=AB=×=，
所以⊙O的半径为．

（3）解：连接OE、OC，
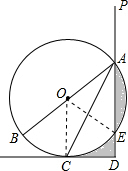
则△OAE为等边三角形，
∴∠AOE=∠AEO=∠COE=60°，
∴扇形AOE的面积=扇形OCE的面积，
∴△AOE和梯形OCDE的高为：•sin60°=×=2，
∴DE=AD-AE=2-=，
所以图中阴影部分的面积=（扇形AOE的面积-△AOE的面积）+（梯形OCDE的面积-扇形OCE的面积）
=扇形AOE的面积-△AOE的面积+梯形OCDE的面积-扇形OCE的面积
=梯形OCDE的面积-△AOE的面积
=×（+）×2-××2=（平方单位），
所以图中阴影部分的面积为（平方单位）．
分析：（1）连接OC，由OA=OC可以得到∠OAC=∠OCA，然后利用角平分线的性质可以证明∠DAC=∠OCA，接着利用平行线的判定即可得到OC∥AD，然后就得到OC⊥CD，由此即可证明直线CD是⊙O的切线；
（2）首先由勾股定理求出AC，再连接BC，根据圆周角定理的推理得到∠ACB=90°，又∠DAC=∠OAC，由此可以得到△ADC∽△ACB，然后利用相似三角形的性质即可解决问题；
（3）连接OE，OC，则三角形OAE为等边三角形，角COE为60度，阴影部分面积可以分别求出：上一部分：是个弓形，圆心角等于60度，半径已经求出，因而面积可以求出，下一部分，用梯形OCDE面积减去扇形OCE面积即可．
点评：此题主要考查了切线的性质与判定，解题时首先利用切线的判定证明切线，然后利用切线的性质及已知条件证明三角形相似即可解决问题．