题目内容
 如图,在边长为1的正方形ABCD中,E为AD边上一点,连接BE,将△ABE沿BE对折,A点恰好落在对角线BD上的点F处.延长AF,与CD边交于点G,延长FE,与BA的延长线交于点H,则下列说法:①△BFH为等腰直角三角形;②△ADF≌△FHA; ③∠DFG=60°;④DE=
如图,在边长为1的正方形ABCD中,E为AD边上一点,连接BE,将△ABE沿BE对折,A点恰好落在对角线BD上的点F处.延长AF,与CD边交于点G,延长FE,与BA的延长线交于点H,则下列说法:①△BFH为等腰直角三角形;②△ADF≌△FHA; ③∠DFG=60°;④DE=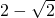 ;⑤S△AEF=S△DFG.
;⑤S△AEF=S△DFG.
其中正确的说法有
- A.1个
- B.2个
- C.3个
- D.4个
D
分析:①由折叠后对称很容易得到结果.②由上一证结论,并证明△AHF≌△ADF从而证得.③由①证得:∠ABE=∠DAG=22.5°,在直角三角形ADG中,角AGD=67.5°故不正确.④根据对折可以证明三角形DEF 是等腰直角三角形,DF= 1,所以DE=
1,所以DE= DF,从而得证.⑤过D作DI垂直于FG,垂足为I,EB与AF的交点为G,证明三角形DFI与EFG全等.
DF,从而得证.⑤过D作DI垂直于FG,垂足为I,EB与AF的交点为G,证明三角形DFI与EFG全等.
解答: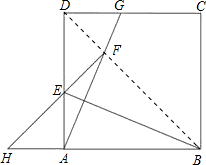 解:由题意三角形ABE对折后为三角EFB,
解:由题意三角形ABE对折后为三角EFB,
∴∠EFB=∠DAB=90°,
由题意正方形ABCD,连接BD,
则角ABF=45°,
∴在直角三角形BHF中HF=BF,
故①正确.
由上一证知:HF=BF=AB,∠FHB=∠ADB=45°,
又知AF为公共边,
∴△AHF≌△ADF,
故②正确.
由①证得:∠ABE=∠DAG=22.5°,
由已知∠BDC=45°,
∴在直角三角形ADG中,角AGD=67.5°,
在三角形DFG中角DFG=67.5°,
故③不正确;
根据对折可以证明三角形DEF 是等腰直角三角形,DF= 1,
1,
所以DE= DF,
DF,
即④正确,
或者过D作FG的垂线证明三角形全等,
⑤过D作DI垂直于FG,垂足为I,EB与AF的交点为G,
而这两个三角形的面积分别等于相应所在三角形的面积的一半,
所以证得三角形DFI与EFG全等.
故⑤正确.
所以①②④⑤正确.
故选D.
点评:本题考查了正方形的性质,①由折叠后对称很容易得到结果.②由上一证结论,并证明△AHF≌△ADF从而证得.③由①证得:∠ABE=∠DAG=22.5°,在直角三角形ADG中,角AGD=67.5°故不正确.④根据对折可以证明三角形DEF 是等腰直角三角形,DF= 1,所以DE=
1,所以DE= DF,从而得证.⑤过D作DI垂直于FG,垂足为I,EB与AF的交点为G证明三角形DFI与EFG全等.
DF,从而得证.⑤过D作DI垂直于FG,垂足为I,EB与AF的交点为G证明三角形DFI与EFG全等.
分析:①由折叠后对称很容易得到结果.②由上一证结论,并证明△AHF≌△ADF从而证得.③由①证得:∠ABE=∠DAG=22.5°,在直角三角形ADG中,角AGD=67.5°故不正确.④根据对折可以证明三角形DEF 是等腰直角三角形,DF=
 1,所以DE=
1,所以DE= DF,从而得证.⑤过D作DI垂直于FG,垂足为I,EB与AF的交点为G,证明三角形DFI与EFG全等.
DF,从而得证.⑤过D作DI垂直于FG,垂足为I,EB与AF的交点为G,证明三角形DFI与EFG全等.解答:
 解:由题意三角形ABE对折后为三角EFB,
解:由题意三角形ABE对折后为三角EFB,∴∠EFB=∠DAB=90°,
由题意正方形ABCD,连接BD,
则角ABF=45°,
∴在直角三角形BHF中HF=BF,
故①正确.
由上一证知:HF=BF=AB,∠FHB=∠ADB=45°,
又知AF为公共边,
∴△AHF≌△ADF,
故②正确.
由①证得:∠ABE=∠DAG=22.5°,
由已知∠BDC=45°,
∴在直角三角形ADG中,角AGD=67.5°,
在三角形DFG中角DFG=67.5°,
故③不正确;
根据对折可以证明三角形DEF 是等腰直角三角形,DF=
 1,
1,所以DE=
 DF,
DF,即④正确,
或者过D作FG的垂线证明三角形全等,
⑤过D作DI垂直于FG,垂足为I,EB与AF的交点为G,
而这两个三角形的面积分别等于相应所在三角形的面积的一半,
所以证得三角形DFI与EFG全等.
故⑤正确.
所以①②④⑤正确.
故选D.
点评:本题考查了正方形的性质,①由折叠后对称很容易得到结果.②由上一证结论,并证明△AHF≌△ADF从而证得.③由①证得:∠ABE=∠DAG=22.5°,在直角三角形ADG中,角AGD=67.5°故不正确.④根据对折可以证明三角形DEF 是等腰直角三角形,DF=
 1,所以DE=
1,所以DE= DF,从而得证.⑤过D作DI垂直于FG,垂足为I,EB与AF的交点为G证明三角形DFI与EFG全等.
DF,从而得证.⑤过D作DI垂直于FG,垂足为I,EB与AF的交点为G证明三角形DFI与EFG全等. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
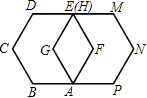 如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点
如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
 如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )
如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( ) 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心, 长为半径作
长为半径作 ,
, ,
,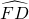 ,求阴影部分的面积.
,求阴影部分的面积. 长为半径作
长为半径作 ,
, ,
, ,求阴影部分的面积.
,求阴影部分的面积.