题目内容

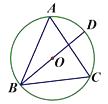
【题目】四个全等的直角三角形按图示方式围成正方形ABCD，过各较长直角边的中点作垂线，围成面积为S的小正方形EFGH．已知AM为Rt△ABM较长直角边，AM＝2EF，则正方形ABCD的面积为（　　）

A. 14SB. 13SC. 12SD. 11S

【答案】B

【解析】

设AM=2a．BM=b．则正方形ABCD的面积=4a2+b2，由题意可知EF=（2a-b）-2（a-b）=2a-b-2a+2b=b，由此即可解决问题．

解：设AM＝2a．BM＝b．则正方形ABCD的面积＝4a2+b2

由题意可知EF＝（2a﹣b）﹣2（a﹣b）＝2a﹣b﹣2a+2b＝b，

∵AM＝2EF，

∴2a＝2b，

∴a＝b，

∵正方形EFGH的面积为S，

∴b2＝S，

∴正方形ABCD的面积＝4a2+b2＝13b2＝13S，

故选：B．

练习册系列答案
相关题目

【题目】如图，△ABC内接于⊙O，BD是直径．若 ，则 等于（ ）

A.
B.
C.
D.

【题目】解方程2x2﹣5x﹣3=0. x2﹣2x=x﹣2．
（1）2x2﹣5x﹣3=0.
（2）x2﹣2x=x﹣2．

【题目】已知，关于x的分式方程＝1．

（1）当m＝﹣1时，请判断这个方程是否有解并说明理由；

（2）若这个分式方程有实数解，求m的取值范围．

【题目】如图，长方形OABC中，O为平面直角坐标系的原点，A点的坐标为（4，0），C点的坐标为（0，6），点B在第一象限内，点P从原点O出发，以每秒2个单位长度的速度沿着O﹣A﹣B﹣C﹣O的路线移动（即沿长方形移动一周）．

（1）写出B点的坐标；

（2）当点P移动3秒时，求三角形OAP的面积；

（3）在移动过程中，当点P到x轴距离为4个单位长度时，求点P移动的时间．

【题目】如果一元一次方程的根是一元一次不等式组的解，则称该一元一次方程为该不等式组的关联方程．

（1）在方程①3x﹣1＝0，②x+1＝0，③x﹣（3x+1）＝﹣5中，不等式组的关联方程是　 　；（填序号）

（2）若不等式组的一个关联方程的根是整数，则这个关联方程可以是　 　；（写出一个即可）

（3）若方程3﹣x＝2x，3+x＝2（x+）都是关于x的不等式组的关联方程，直接写出m的取值范围．

【题目】细心观察图形，认真分析各式，然后解答问题．

OA22＝，；

OA32＝12+，；

OA42＝12+，…

（1）请用含有n（n是正整数）的等式表示上述变规律：OAn2等于多少；Sn等于多少．

（2）求出OA10的长．

（3）若一个三角形的面积是，计算说明他是第几个三角形？

（4）求出S12+S22+S32+…+S102的值．

【题目】如图，在折纸活动中，小李制作了一张△ABC的纸片，点D，E分别在边AB，AC上，将△ABC沿着DE折叠压平，A与A'重合．

（1）若∠B＝50°，∠C＝60°，求∠A的度数；

（2）若∠1+∠2＝130°，求∠A的度数．

【题目】如图，在平面直角坐标系中，直线交x轴于点A，交y轴于点B，交直线于点C，点D与点B关于x轴对称，连接AD交直线于点E．

填空：______．

求直线AD的解析式；

在x轴上存在一点P，则的和最小为______；直接填空即可

当时，点Q为y轴上的一个动点，使得为等腰直角三角形，求点Q的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网