Question

【题目】已知△ABC是等边三角形．
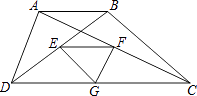
（1）动手操作：如图1，点D在△ABC内，且∠BDC=150°，CD=1，BD= ， 把△BCD绕着点C顺时针旋转，使点B旋转到点A，得到△AEC．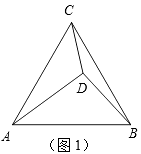

①依题意补全图1；（确认无误后，请用黑色水笔描黑）
②连接DE，则线段DE= ， AD=；
（2）应用拓展：如图2，点D在△ABC外，且CD=3，BD=4，AD=5，求∠BDC的度数．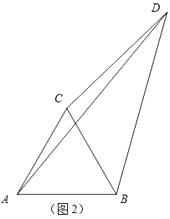

Answer 1

【答案】
（1）解：补全图形如下图：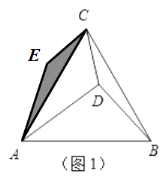
；1；
（2）

解：把△BCD绕着点C顺时针旋转，使点B旋转到点A，得到△ACF，连接DF．

∴∠DCF=∠BCA=60°，CF=CD=3，AF=BD=4

∴△CDF是等边三角形，∴DF=CD=3，∠CFD=60°

∵AD2=52=25，AF2+DF2=42+32=25

∴AD2= AF2+DF2，∴∠AFD=90°

∴∠AFC=∠AFD-∠CFD=90°-60°=30°

∴∠BDC=∠AFC=30° .

答：∠BDC的度数是30° .

【解析】本题在作旋转图形时，注意找准旋转中心、旋转方向、旋转角度三要素. 第2题利用旋转的性质和线段之间的关系，通过勾股定理的逆定理求解即可.
【考点精析】关于本题考查的等边三角形的性质和勾股定理的逆定理，需要了解等边三角形的三个角都相等并且每个角都是60°；如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形才能得出正确答案．