Question

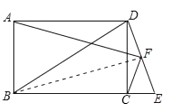
【题目】已知，矩形ABCD中，延长BC至E，连接DE，F为DE的中点，连结AF、CF且AF⊥CF.

求证：(1)∠ADF=∠BCF；

(2)BD=AD+CE.

Answer 1

【答案】见解析

【解析】

（1）根据F为中点得到CF=DF=EF,再得到∠CDF=∠DCF,再利用矩形的性质即可求解；

（2）先根据全等三角形的判定与性质得到△BDE为等腰三角形，再根据线段之间的关系即可证明.

（1）在矩形ABCD中，

∵AD＝BC，∠ADC＝∠BCD＝90°，

∴∠DCE＝90°，

在Rt△DCE中，

∵F为DE中点，

∴DF＝CF，

∴∠CDF=∠DCF,

∴∠ADC＋∠CDF＝∠BCD＋∠DCF，

即∠ADF＝∠BCF；

（2）连接BF，

在△AFD和△BFC中

，

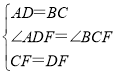∴△ADF≌△BCF，

∴∠AFD=∠BFC,

∵AF⊥CF，

∴∠AFD+∠AFB =∠BFC+∠AFB=90°

∴BF⊥DE，

∵F为DE中点，

在△BDF和△BEF中

，

∴△ADF≌△BCF，

∴BD=BE

∵BE=BC+CE

∴BD=BC+CE= AD+CE.

故BD=AD+CE.