题目内容
【题目】(1)如图1,Rt△ABC中,若AC=4,BC=3,DE⊥AC,且DE=DB,求AD的长;
(2)如图2,已知△ABC,若AB边上存在一点M,若AC边上存在一点N,使MB=MN,且△AMN∽△ABC,请利用没有刻度的直尺和圆规,作出符合条件的线段MN(注:不写作法,保留作图痕迹,对图中涉及到的点用字母进行标注).
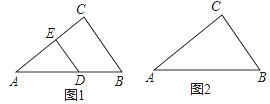
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)根据DE∥BC,得出△ADE∽△ABC,进而得到![]() ,据此可得AD的长.
,据此可得AD的长.
(2)作∠B的平分线BN,交AC于G,作BN的垂直平分线MG,交AB于M,则MN=BM,而MN∥BC,则△AMN∽△ABC.
(1)在Rt△ABC中,AC=4,BC=3,
∴AB=5,
∵DE⊥AC,∠C=90°,
∴DE∥BC,
∴△ADE∽△ABC,
∴![]() ,
,
即![]() ,
,
解得AD=![]() ,
,
故AD的长为![]() .
.
(2)如图2所示,作∠B的平分线BN,交AC于G,作BN的垂直平分线MG,交AB于M,MN即为所求.

练习册系列答案
相关题目




