题目内容
【题目】有一个抛物线型蔬菜大棚,将其截面放在如图所示的平面直角坐标系中,抛物线可以用函数y=ax2+bx来表示.已知大棚在地面上的宽度OA为8米,距离O点2米处的棚高BC为![]() 米.
米.
(1)求该抛物线的函数关系式;
(2)若借助横梁DE建一个门,要求门的高度不低于1.5米,则横梁DE的宽度最多是多少米?

【答案】(1)y=-![]() x2+
x2+![]() x;(2)横梁DE的宽度最多是4
x;(2)横梁DE的宽度最多是4![]() 米.
米.
【解析】
(1)直接利用待定系数法求出二次函数解析式进而得出答案;
(32)利用y=1.5代入求出答案.
(1)由题意可得,抛物线经过(2,![]() ),(8,0),
),(8,0),
∴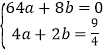 ,
,
解得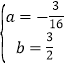
∴y=-![]() x2+
x2+![]() x;
x;
(2)由题意可得:当y=1.5时,1.5=-![]() x2+
x2+![]() x,
x,
解得x1=4+2![]() ,x2=4-2
,x2=4-2![]() .
.
故DE=|x1-x2|=|4+2![]() -(4-2
-(4-2![]() )|=4
)|=4![]() .
.
即横梁DE的宽度最多是4![]() 米.
米.

练习册系列答案
相关题目