题目内容
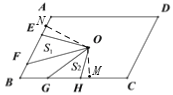
【题目】点O是平行四边形ABCD的对称中心,AD>AB,E、F分别是AB边上的点,且EF=![]() AB;G、H分别是BC边上的点,且GH=
AB;G、H分别是BC边上的点,且GH=![]() BC;若S1,S2分别表示EOF和GOH的面积,则S1,S2之间的等量关系是______________
BC;若S1,S2分别表示EOF和GOH的面积,则S1,S2之间的等量关系是______________

【答案】2S1=3S2
【解析】
过点O分别作OM⊥BC,垂足为M,作ON⊥AB,垂足为N,根据点O是平行四边形ABCD的对称中心以及平行四边形的面积公式可得ABON=BCOM,再根据S1=![]() EFON,S2=
EFON,S2=![]() GHOM,EF=
GHOM,EF=![]() AB,GH=
AB,GH=![]() BC,则可得到答案.
BC,则可得到答案.
过点O分别作OM⊥BC,垂足为M,作ON⊥AB,垂足为N,
∵点O是平行四边形ABCD的对称中心,
∴S平行四边形ABCD=AB2ON, S平行四边形ABCD=BC2OM,
∴ABON=BCOM,
∵S1=![]() EFON,S2=
EFON,S2=![]() GHOM,EF=
GHOM,EF=![]() AB,GH=
AB,GH=![]() BC,
BC,
∴S1=![]() ABON,S2=
ABON,S2=![]() BCOM,
BCOM,
∴2S1=3S2,
故答案为:2S1=3S2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目