题目内容
如图,已知,四边形ABCD为菱形,点E、F分别是线段DC和BC延长线的点,AE与BC交于点M,AF与CD交于点N,且∠BAD=2∠EAF.
(1)当∠B=60°,如图1,求证:CE•CF=AB2;
(2)当∠B=90°,如图2,则线段CE、CF、AB之间的数量关系是
(3)在(1)的条件下,若CM:CF=1:6,S 四边形AMCN=9
,求tan∠F的值.

(1)当∠B=60°,如图1,求证:CE•CF=AB2;
(2)当∠B=90°,如图2,则线段CE、CF、AB之间的数量关系是
2AB2=CE•CF
2AB2=CE•CF
;(3)在(1)的条件下,若CM:CF=1:6,S 四边形AMCN=9
| 3 |

分析:(1)如图1,连接AC,由菱形的性质可以得出△ABC是等边三角形,进而就可以得出△ACE∽△FCA,由相似三角形的性质就可以得出结论;
(2)如图2,连接AC,可以得出△ACE∽△FCA,就可以得出AC2=CF•CE,由勾股定理就可以求出2AB2=CE•CF;
(3)如图1,作AG⊥BC于G,NH⊥CF与H,根据条件可以得出△ABM≌△ACN,△ACM≌△ADN,就可以得出S四边形AMCN=S△ABC,就可以求出菱形的边长,设MC=a,FC=6a,由△AMF的面积-△CNF的面积=S四边形AMCN,就可以得出求出a值,进而就可以求出GF的值而求出结论.
(2)如图2,连接AC,可以得出△ACE∽△FCA,就可以得出AC2=CF•CE,由勾股定理就可以求出2AB2=CE•CF;
(3)如图1,作AG⊥BC于G,NH⊥CF与H,根据条件可以得出△ABM≌△ACN,△ACM≌△ADN,就可以得出S四边形AMCN=S△ABC,就可以求出菱形的边长,设MC=a,FC=6a,由△AMF的面积-△CNF的面积=S四边形AMCN,就可以得出求出a值,进而就可以求出GF的值而求出结论.
解答:解:(1)如图1,连接AC,
∵四边形ABCD是菱形,
∴AB=BC=CD=DA.AB∥CD,AD∥BC.
∴∠B+∠DAB=180°,∠B+∠BCD=180°.
∵∠B=60°,
∴∠BAD=∠BCD=120°,
∴∠ACB=∠BAC=∠DAC=∠ACD=60°,
∴∠BAM+∠CAM=60°,∠DAN+∠CAN=60°.
∵∠B=60°,
∴∠ACB=∠BAC=∠B,
∴△ABC是等边三角形,
∴AB=BC=AC.
∵∠BAD=2∠EAF,
∴∠EAF=60°.
∴∠EAC+∠FAC=60°.
∵∠FAC+∠F=∠ACB=60°,
∴∠EAC=∠F.
∵∠BCE=∠DCF,且∠ACB=∠ACD=60°,
∴∠ACE=∠ACF,
∴△ACE∽△FCA,
∴
=
,
∴AC2=CE•CF,
∴CE•CF=AB2;
(2)2AB2=CE•CF
如图2,连接AC,
∵四边形ABCD是菱形,
∴AB=BC=CD=DA.AB∥CD,AD∥BC.
∴∠B+∠DAB=180°,∠B+∠BCD=180°.
∵∠B=90°,
∴∠BAD=∠BCD=90°,
∴∠ACB=∠BAC=∠DAC=∠ACD=45°,
∴∠BAM+∠CAM=45°,∠DAN+∠CAN=45°.
∵∠B=90°,
∴△ABC是等腰直角三角形,
∴AC2=AB2+BC2,
∴AC2=2AB2.
∵∠BAD=2∠EAF,
∴∠EAF=60°.
∴∠EAC+∠FAC=45°.
∵∠FAC+∠F=∠ACB=45°,
∴∠EAC=∠F.
∵∠BCE=∠DCF,且∠ACB=∠ACD=45°,
∴∠ACE=∠ACF,
∴△ACE∽△FCA,
∴
=
,
∴AC2=CE•CF,
∴2AB2=CE•CF;
(3)如图1,作AG⊥BC于G,NH⊥CF与H,
∴∠AGB=∠NHC=90°.
∵∠B=∠NCH=60°,
∴∠BAG=∠CNH=30°,
∴BG=
AB,CH=
CN.
∴AG=
BG,NH=
CH.
∵∠BAM+∠CAM=60°,∠DAN+∠CAN=60°,
∴∠BAM=∠CAN,∠CAM=∠DAN.
在△ABM和△ACN中
,
∴△ABM≌△ACN(ASA),
∴S△ABM=S△ACN.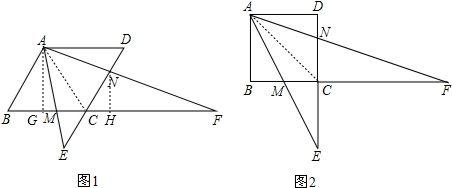
∴S四边形AMCN=S△ABC=9
,
∴
BC•AG=9
.
设AB=BC=a,
∴BG=
a,AG=
a.
∴
×
a×a=9
,
解得:a=6.
∴AG=3
,BG=3.
在△ACM和△ADN中
,
∴△ACM≌△ADN(ASA)
∴MC=ND.
∵CM:CF=1:6,设CM=x,则CF=6x,CN=6-x,
∴CH=
,NH=
∴
×7x×3
-6x×
×
=9
,
解得:x1=-3(舍去),x2=2.
∴CF=12,
∴GF=15.
∴tan∠F=
=
.
∵四边形ABCD是菱形,
∴AB=BC=CD=DA.AB∥CD,AD∥BC.
∴∠B+∠DAB=180°,∠B+∠BCD=180°.
∵∠B=60°,
∴∠BAD=∠BCD=120°,
∴∠ACB=∠BAC=∠DAC=∠ACD=60°,
∴∠BAM+∠CAM=60°,∠DAN+∠CAN=60°.
∵∠B=60°,
∴∠ACB=∠BAC=∠B,
∴△ABC是等边三角形,
∴AB=BC=AC.
∵∠BAD=2∠EAF,
∴∠EAF=60°.
∴∠EAC+∠FAC=60°.
∵∠FAC+∠F=∠ACB=60°,
∴∠EAC=∠F.
∵∠BCE=∠DCF,且∠ACB=∠ACD=60°,
∴∠ACE=∠ACF,
∴△ACE∽△FCA,
∴
| AC |
| FC |
| CE |
| AC |
∴AC2=CE•CF,
∴CE•CF=AB2;
(2)2AB2=CE•CF
如图2,连接AC,
∵四边形ABCD是菱形,
∴AB=BC=CD=DA.AB∥CD,AD∥BC.
∴∠B+∠DAB=180°,∠B+∠BCD=180°.
∵∠B=90°,
∴∠BAD=∠BCD=90°,
∴∠ACB=∠BAC=∠DAC=∠ACD=45°,
∴∠BAM+∠CAM=45°,∠DAN+∠CAN=45°.
∵∠B=90°,
∴△ABC是等腰直角三角形,
∴AC2=AB2+BC2,
∴AC2=2AB2.
∵∠BAD=2∠EAF,
∴∠EAF=60°.
∴∠EAC+∠FAC=45°.
∵∠FAC+∠F=∠ACB=45°,
∴∠EAC=∠F.
∵∠BCE=∠DCF,且∠ACB=∠ACD=45°,
∴∠ACE=∠ACF,
∴△ACE∽△FCA,
∴
| AC |
| FC |
| CE |
| AC |
∴AC2=CE•CF,
∴2AB2=CE•CF;
(3)如图1,作AG⊥BC于G,NH⊥CF与H,
∴∠AGB=∠NHC=90°.
∵∠B=∠NCH=60°,
∴∠BAG=∠CNH=30°,
∴BG=
| 1 |
| 2 |
| 1 |
| 2 |
∴AG=
| ||
| 2 |
| ||
| 2 |
∵∠BAM+∠CAM=60°,∠DAN+∠CAN=60°,
∴∠BAM=∠CAN,∠CAM=∠DAN.
在△ABM和△ACN中
|
∴△ABM≌△ACN(ASA),
∴S△ABM=S△ACN.

∴S四边形AMCN=S△ABC=9
| 3 |
∴
| 1 |
| 2 |
| 3 |
设AB=BC=a,
∴BG=
| 1 |
| 2 |
| ||
| 2 |
∴
| 1 |
| 2 |
| ||
| 2 |
| 3 |
解得:a=6.
∴AG=3
| 3 |
在△ACM和△ADN中
|
∴△ACM≌△ADN(ASA)
∴MC=ND.
∵CM:CF=1:6,设CM=x,则CF=6x,CN=6-x,
∴CH=
| 6-x |
| 2 |
| ||
| 2 |
∴
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
解得:x1=-3(舍去),x2=2.
∴CF=12,
∴GF=15.
∴tan∠F=
3
| ||
| 15 |
| ||
| 5 |
点评:本题考查了菱形的性质的运用,等腰直角三角形的性质的运用,相似三角形的判定及性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,三角形的面积公式的运用等边三角形的判定及性质的运用,解答时证明三角形相似和全等是关键.

练习册系列答案
相关题目
 如图,已知在四边形ABCD中,E、F分别为AD、DC的中点,AD∥BC,AD:DC=1:
如图,已知在四边形ABCD中,E、F分别为AD、DC的中点,AD∥BC,AD:DC=1: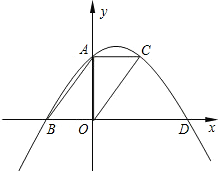 如图,已知平行四边形ABOC的顶点A、B、C在二次函数y=ax2+bx+c的图象上,又点A、B分别在y轴和x轴上,∠ABO=45°.图象顶点的横坐标为2,求二次函数解析式.
如图,已知平行四边形ABOC的顶点A、B、C在二次函数y=ax2+bx+c的图象上,又点A、B分别在y轴和x轴上,∠ABO=45°.图象顶点的横坐标为2,求二次函数解析式.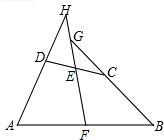 如图,已知:四边形ABCD中,AD=BC,E、F分别是DC、AB的中点,直线EF分别与BC、AD的延长线相交于G、H.求证:∠AHF=∠BGF.
如图,已知:四边形ABCD中,AD=BC,E、F分别是DC、AB的中点,直线EF分别与BC、AD的延长线相交于G、H.求证:∠AHF=∠BGF.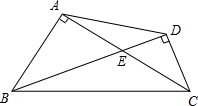 (2013•奉贤区一模)如图,已知在四边形ABCD中,AC⊥AB,BD⊥CD,AC与BD相交于点E,S△AED=9,S△BEC=25.
(2013•奉贤区一模)如图,已知在四边形ABCD中,AC⊥AB,BD⊥CD,AC与BD相交于点E,S△AED=9,S△BEC=25. 如图,已知平行四边形ABCD,点E是AD边上的点,且AE=2ED,连接BE并延长交CD的延长线于点F,
如图,已知平行四边形ABCD,点E是AD边上的点,且AE=2ED,连接BE并延长交CD的延长线于点F,