题目内容
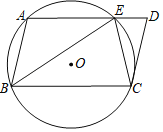
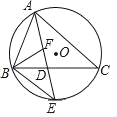
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,∠ABC的平分线BF交AD于点F,交BC于点D.
(1)求证:BE=EF;
(2)若DE=4,DF=3,求AF的长.
【答案】(1)见解析;(2)AF=![]() .
.
【解析】
(1)通过证明∠6=∠EBF得到EB=EF;
(2)先证明△EBD∽△EAB,再利用相似比求出AE,然后计算AE-EF即可得到AF的长.
(1)证明:∵AE平分∠BAC,
∴∠1=∠4,
∵∠1=∠5,
∴∠4=∠5,
∵BF平分∠ABC,
∴∠2=∠3,
∵∠6=∠3+∠4=∠2+∠5,
即∠6=∠EBF,
∴EB=EF;
(2)解:∵DE=4,DF=3,
∴BE=EF=DE+DF=7,
∵∠5=∠4,∠BED=∠AEB,
∴△EBD∽△EAB,
![]() ,即
,即![]() ,
,
∴EA=![]() ,
,
∴AF=AE﹣EF=![]() .
.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目