题目内容
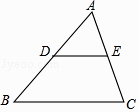
【题目】2017宁夏）在边长为2的等边三角形ABC中，P是BC边上任意一点，过点 P分别作 PM⊥A B，PN⊥AC，M、N分别为垂足． 
（1）求证：不论点P在BC边的何处时都有PM+PN的长恰好等于三角形ABC一边上的高；
（2）当BP的长为何值时，四边形AMPN的面积最大，并求出最大值．
【答案】
（1）解：连接AP，过C作CD⊥AB于D，
∵△ABC是等边三角形，
∴AB=AC，
∵S△ABC=S△ABP+S△ACP，
∴ 
ABCD= ABPM+ ACPN，
∴PM+PN=CD，
即不论点P在BC边的何处时都有PM+PN的长恰好等于三角形ABC一边上的高；
（2）解：设BP=x，则CP=2﹣x，
∵△ABC是等边三角形，
∴∠B=∠C=60°，
∵PM⊥AB，PN⊥AC，
∴BM= x，PM= 
x，CN= （2﹣x），PN= （2﹣x），
∴四边形AMPN的面积= ×（2﹣ x） x+ 
[2﹣ （2﹣x）] （2﹣x）=﹣ 
x2+ x+ =﹣ （x﹣1）2+ 
，
∴当BP=1时，四边形AMPN的面积最大，最大值是
【解析】（1）连接AP，过C作CD⊥AB于D，根据等边三角形的性质得到AB=AC，根据三角形的面积公式列方程即可得到结论；（2）设BP=x，则CP=2﹣x，由△ABC是等边三角形，得到∠B=∠C=60°，解直角三角形得到BM= x，PM= x，CN= （2﹣x），PN= （2﹣x），根据二次函数的性质即可得到结论．
【考点精析】解答此题的关键在于理解二次函数的最值的相关知识，掌握如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-2)/4a，以及对等边三角形的性质的理解，了解等边三角形的三个角都相等并且每个角都是60°．
