题目内容
【题目】(如图①,将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点 M处,点C落在点N处,MN与CD交于点P, 连接EP.
⑴如图②,若M为AD边的中点,①△AEM的周长=_________cm;②求证:EP=AE+DP;
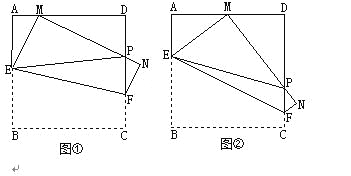
⑵随着落点M在AD边上取遍所有的位置(点M不与A、D重合),△PDM的周长是否发生变化?请说明理由.
【答案】(1)①6 ②见解析(2)△PDM的周长保持不变,理由见解析
【解析】
(1)①由折叠知BE=EM,AE+EM+AM=AE+EB+AM=AB+AM,根据边长及中点易求周长;②取EP中点G,连接MG,再根据梯形中位线与三角形中位线解答即可;(2)不变化,可证△AEM∽△DMP,两个三角形的周长比为AE:MD,设AM=x,根据勾股定理可以用x表示MD的长与△MAE的周长,再根据周长比等于相似比,即可求解.
(1)①由折叠可知,BE=BM,∠B=∠MEP=90°,
△AEM的周长= AE+EM+AM=AE+EB+AM=AB+AM.
∵AB=4,M是AD中点,
∴△AEM的周长=6(cm)
②证明:取EP中点G,连接MG,在梯形AEPD中
∵M、G分别为AD、EP的中点
∴![]()
由折叠,得∠EMP=∠B=90°
又G为EP的中点
∴MG=![]() EP
EP
∴EP="AE+DP"

(2)△PDM的周长保持不变
证明:设AM=xcm,则DM=(4-x)cm
Rt△EAM中,由![]()
![]()
∵∠AME+∠AEM=90°
∠AME+∠PMD=90°
∴∠AEM=∠PMD
又∵∠A=∠D=90°
∴△PDM∽△MAE
∴![]()
即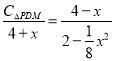
∴
∴△PDM的周长保持不变.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目