题目内容
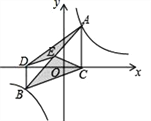
【题目】如图①,![]() 为坐标原点,点
为坐标原点,点![]() 在
在![]() 轴的正半轴上,四边形
轴的正半轴上,四边形![]() 是四边形,
是四边形,![]() ,反比例函数
,反比例函数![]() 在第一象限内的图像经过点
在第一象限内的图像经过点![]() ,与
,与![]() 交于点
交于点![]()
(1)若![]() ,求反比例函数解析式;
,求反比例函数解析式;
(2)若点![]() 为
为![]() 的中点,且
的中点,且![]() 的面积
的面积![]() ,求
,求![]() 的长和点
的长和点![]() 的坐标;
的坐标;
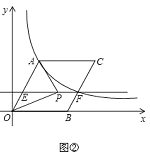
(3)在(2)中的条件下,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() (如图②),点
(如图②),点![]() 为直线
为直线![]() 上的一个动点,连接
上的一个动点,连接![]() ,是否存在这样的点
,是否存在这样的点![]() ,使以
,使以![]() 为顶点的三角形的直角三角形?若存在,请直接写出所有点
为顶点的三角形的直角三角形?若存在,请直接写出所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() ;C(
;C(![]() ,
,![]() );(3) P
);(3) P![]() 或
或![]() .
.
【解析】
(1)根据sin∠AOB=![]() ,OA=5,可知点A的坐标,代入解析式求解.
,OA=5,可知点A的坐标,代入解析式求解.
(2)根据反比例函数″k″的几何意义,转化三角形的面积,列式求解即可.
(3)分两种情况,以A为直角顶点和以O为直角顶点,构造″K″字形相似,列出比例关系可以求出点P的坐标.
解:(1) 过点![]() 作
作![]() 于
于![]() ,
,
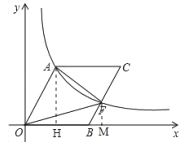
∵![]() ,
,![]() ,
,
![]() 点坐标为
点坐标为![]() ,
,
![]() 反比例函数解析式:
反比例函数解析式:![]()
(2)设![]() ,如图2,过点
,如图2,过点![]() 作
作![]() 轴于
轴于![]() ,过点C作CN⊥x轴于点N,
,过点C作CN⊥x轴于点N,
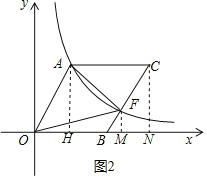
由平行四边形性质可知OH=BN,
∵sin∠AOB=![]() ,
,
![]() ,
,
![]() ,
,
∵S△AOF=12,
∴S四边形AOBC=24,
∵F为BC的中点,
∴S△OBF=6,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
∵S四边形AOBC=24,
![]()
![]()
![]()
(3) 存在两种情况,
①A为直角顶点,如图3所示,
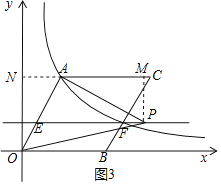
![]() ),点F为BC中点,
),点F为BC中点,
∴点F的纵坐标为![]() ,
,
∵EF∥OB,点P在直线EF上,
∴点P的纵坐标为![]() ,
,
过点P作PM⊥AC于点M,过点A作AN⊥y轴于点N,
则PM=![]() ,
,
∵∠OAP=90°,
∴△OAN∽△APM,
![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
②以O为直角顶点时,如图4所示,
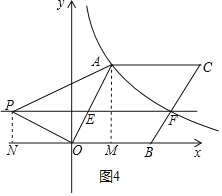
过点P作PN⊥x轴于点N,过点A作AM⊥x轴于点M,
则![]() ,
,
∵∠AOP=90°,
则△PON∽△AOM,
![]() ,即
,即![]() ,
,
![]() ,
,
∴点P![]() ,
,
综上所述:点P![]() 或
或![]() .
.

【题目】为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元) | 5 | 10 | 20 | 50 | 100 |
人数(单位:个) | 2 | 4 | 5 | 3 | 1 |
关于这15名同学所捐款的数额,下列说法正确的是
A.众数是100 B.平均数是30 C.极差是20 D.中位数是20