题目内容
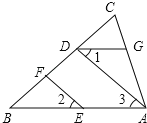
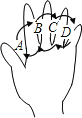
【题目】右图为手的示意图，在各个手指间标记字母A、B、C、D．请你按图中箭头所指方向（即ABCDCBABC…的方式）从A开始数连续的正整数1，2，3，4…，当数到12时，对应的字母是 ；当字母C第201次出现时，恰好数到的数是 ；当字母C第2n+1次出现时（n为正整数），恰好数到的数是 （用含n的代数式表示）．
【答案】B；603；6n+3
【解析】解：通过对字母观察可知：前六个字母为一组，后边就是这组字母反复出现．
当数到12时，因为12除以6刚好余数为零，则表示这组字母刚好出现两次，所以最后一个字母应该是B．
当字母C第201次出现时，由于每组字母中C出现两次，则这组字母应该出现100次后还要加一次C字母出现，
而第一个C字母在第三个出现，所以应该是100×6+3=603．
当字母C第2n+1次出现时，则这组字母应该出现n次后还要加一次C字母出现，所以应该是n×6+3=6n+3．
故答案为：B；603；6n+3．
练习册系列答案
轻松暑假总复习系列答案
相关题目
【题目】甲，乙两支仪仗队队员的身高（单位：cm）如下：
甲队：178，177，179，178，177，178，177，179，178，179；
乙队：178，179，176，178，180，178，176，178，177，180；
（1）将下表填完整：
身高 | 176 | 177 | 178 | 179 | 180 |
甲队（人数） | 3 | 4 | |||
乙队（人数） | 2 | 1 | 1 |
（2）甲队队员身高的平均数为 cm，乙队队员身高的平均数为 cm；
（3）你认为哪支仪仗队更为整齐？简要说明理由．
