题目内容
【题目】若点A(3,3 )是正比例函数![]() 上一点,点M(m ,0)与点N(0 ,n)分别在x轴与y轴上,且∠MAN=90°.
上一点,点M(m ,0)与点N(0 ,n)分别在x轴与y轴上,且∠MAN=90°.
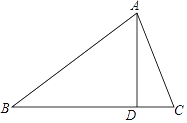
(1)如图1,当N点与原点O重合,求M点的坐标;
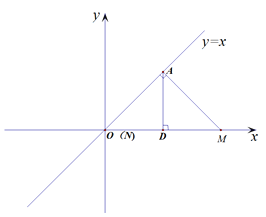
(2)如图2,已知m,n都为正数,连接MN,若MN=![]() ,求△MON的面积.
,求△MON的面积.

【答案】(1)M点坐标为(6,0);(2)![]()
【解析】试题分析:(1)过点A作AD⊥x轴于D,由点A的坐标即可得出AD=OD=3,进而得出∠AOD=∠OAD=45°,再通过角的计算得出∠AMO=45°,从而得出AO=AM,根据等腰三角形的性质即可得出OM=2OD,由此即可得出点M的坐标;(2)过点A作AQ⊥x轴于Q,作AP⊥y轴于P,由点A的坐标结合矩形的性质即可得出四边形APOQ是正方形,根据正方形的性质找出AP=AQ,再根据全等三角形的判定定理(ASA)即可证出△APN≌△AQM,从而得出PN=QM,通过边与边之间的关系结合勾股定理即可得出mn的值,将其代入三角形的面积公式即可得出结论.
试题解析:(1) 当N点与原点O重合时,如图作AD⊥x轴于D,
∵ A(3,3)
∴ AD=OD=3
∴ ∠AOD=∠OAD=45°
又∵∠MAN=90°
∴∠AMO=90°-45°=45°
∴ AO=AM,
∴OM=2OD=6
∴ M点坐标为(6,0)
(2)如图作AQ⊥![]() 轴于Q,AP⊥
轴于Q,AP⊥![]() 轴于P,
轴于P,
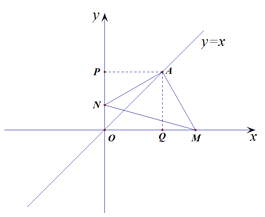
则 ∠APO=∠AQO=90°
又∵∠POQ=90°
∴ 四边形APOQ是矩形,
∵ A(3,3),
∴ OP=OQ=3,
∴ 四边形APOQ是正方形,
∴ AP=AQ.
∵ ∠PAN+∠NAQ=90°, ∠QAM+∠NAQ=90°,
∴ ∠PAN=∠QAM.
∴ △APN ≌ △AQM ,
∴ PN=QM.
∵M (m , 0), N (0 , n)
∴ ON=n,OM=m,
∴ PM=3-n,QM=m-3,
∴ 3-n=m-3,即![]() .
.
在Rt△MON中, ![]()
∴![]() ,即
,即![]()
∵![]() ,
,
∴![]() ,即
,即![]()
∴![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案