��Ŀ����
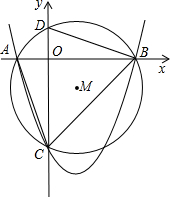 ��ͼ����֪������y=ax2+bx-3��x�ύ��A��B���㣬��y�ύ��C�㣬����A��B��C�����Բ��Բ��M��1��m��ǡ���ڴ������ߵĶԳ����ϣ���M�İ뾶Ϊ
��ͼ����֪������y=ax2+bx-3��x�ύ��A��B���㣬��y�ύ��C�㣬����A��B��C�����Բ��Բ��M��1��m��ǡ���ڴ������ߵĶԳ����ϣ���M�İ뾶Ϊ| 5 |
��1����m��a��b��ֵ��
��2��������P�ӵ�C���������߶�CB��ÿ��2����λ�����ٶ��˶�������P��y���ƽ���߽���������Q������P�˶�����ʱ���߶�PQ��ֵ������ʱP�����ꣻ
��3���ڣ�2�������£����߶�PQ��ֵ���ʱ���ı���ACQB����Ƿ�Ҳ���˵�����ɣ�
��������1��ͨ�������ߵĽ���ʽ��������ȷ������OC�ij�����֪��M�İ뾶������M��y��Ĵ��ߣ�ͨ��������ֱ����������ȷ����M�������ꣻͬ������M��x��Ĵ��ߺ�������B�����꣬��A��B���������ߵĶԳ���Գƣ�����Բ�������ߵĶԳ��ԣ���M�����������߶Գ����ϣ�����ȷ����A����������ô���ϵ�����������a��b��ֵ��
��2���������ֱ��BC�Ľ���ʽ������ֱ��BC�������ߵĽ���ʽ���ȱ�ʾ����P��Q�����꣬����������IJΪ�߶�PQ�ij����������ú��������ʼ��ɵý⣮
��3���ı���ACQB�У��ɷ��������ֶԴ�����ABC����BCQ��ǰ�ߵ�����Ƕ�ֵ�����ı��ε���������ô��BCQ������������������PQ��OB����B��C�������ľ���ֵ����һ�룬OB�Ƕ�ֵ����ȻPQ���ʱ���ı��ε����Ҳ�����ģ�
��2���������ֱ��BC�Ľ���ʽ������ֱ��BC�������ߵĽ���ʽ���ȱ�ʾ����P��Q�����꣬����������IJΪ�߶�PQ�ij����������ú��������ʼ��ɵý⣮
��3���ı���ACQB�У��ɷ��������ֶԴ�����ABC����BCQ��ǰ�ߵ�����Ƕ�ֵ�����ı��ε���������ô��BCQ������������������PQ��OB����B��C�������ľ���ֵ����һ�룬OB�Ƕ�ֵ����ȻPQ���ʱ���ı��ε����Ҳ�����ģ�
���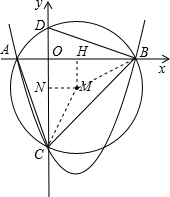 �⣺��1����MN��CD��N��MH��AB��H���ֱ�����MC��MB��
�⣺��1����MN��CD��N��MH��AB��H���ֱ�����MC��MB��
�ߡ�M�İ뾶Ϊ
��xM=1��
��CN=2��ON=1��BH=2��OB=3��
��m=-1��
��Բ��M��1��m��ǡ���ڴ������ߵĶԳ����ϣ�
��OA=1��A��-1��0����B��3��0����
����y=ax2+bx-3�ã�
��
���
��
����m=-1��a=1��b=-2��
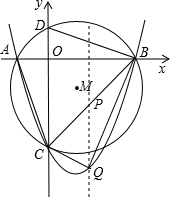 ��2�����P�˶���ʱ��Ϊt�룬��CP=2t��
��2�����P�˶���ʱ��Ϊt�룬��CP=2t��
�֡�OC=OB��
���OBC=��OCB=45�㣬
��xP=
t��
��֪��ֱ��BC�Ľ���ʽΪ y=x-3
���P��
t��
t-3����
��PQ��y�ᣬ
��Q��
t��2t2-2
t-3����
PQ=
t-3-��2t2-2
t-3��=-2t2+3
t=-2��t-
��2+
��
����P�˶�
�룬�߶�PQ��ֵ���
�ʴ�ʱ��P������Ϊ��
��-
����
��3�����߶�PQ��ֵ����ǣ��ı���ACQB�����������ɣ�
S�ı���ACQB=S��ABC+S��CQB��
����S��ABC=
AB��OC=
��4��3=6��Ϊ��ֵ��
��S��CQB=
��|xB-xC|��PQ=
��3��PQ=
PQ
���߶�PQ��ֵ���ʱ����CQB���������ı���ABCQ��������
 �⣺��1����MN��CD��N��MH��AB��H���ֱ�����MC��MB��
�⣺��1����MN��CD��N��MH��AB��H���ֱ�����MC��MB���ߡ�M�İ뾶Ϊ
| 5 |
��CN=2��ON=1��BH=2��OB=3��
��m=-1��
��Բ��M��1��m��ǡ���ڴ������ߵĶԳ����ϣ�
��OA=1��A��-1��0����B��3��0����
����y=ax2+bx-3�ã�
|
���
|
����m=-1��a=1��b=-2��
 ��2�����P�˶���ʱ��Ϊt�룬��CP=2t��
��2�����P�˶���ʱ��Ϊt�룬��CP=2t���֡�OC=OB��
���OBC=��OCB=45�㣬
��xP=
| 2 |
��֪��ֱ��BC�Ľ���ʽΪ y=x-3
���P��
| 2 |
| 2 |
��PQ��y�ᣬ
��Q��
| 2 |
| 2 |
PQ=
| 2 |
| 2 |
| 2 |
3
| ||
| 4 |
| 9 |
| 4 |
����P�˶�
3
| ||
| 4 |
�ʴ�ʱ��P������Ϊ��
| 3 |
| 2 |
| 3 |
| 2 |
��3�����߶�PQ��ֵ����ǣ��ı���ACQB�����������ɣ�
S�ı���ACQB=S��ABC+S��CQB��
����S��ABC=
| 1 |
| 2 |
| 1 |
| 2 |
��S��CQB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
���߶�PQ��ֵ���ʱ����CQB���������ı���ABCQ��������
������������Ҫ������ǣ���������ʽ��ȷ����Բ�ĶԳ��ԡ����ɶ�����Ӧ���Լ�ͼ������Ľⷨ���ص�֪ʶ���ڽ���������һ����������ʱ����������ͼ�μ�����ĺͲ��ϵ�dz��õķ�����

��ϰ��ϵ�д�
�����Ŀ
 C��0��3����
C��0��3���� ��C��0��-3�����㣬��x�ύ����һ��B��
��C��0��-3�����㣬��x�ύ����һ��B�� ��2013•��������ͼ����֪�����߾���A��1��0����B��0��3�����㣬�Գ�����x=-1��
��2013•��������ͼ����֪�����߾���A��1��0����B��0��3�����㣬�Գ�����x=-1�� ��ͼ����֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=1���������߾���A��-1��0����C��0��-3�����㣬��x�ύ����һ��B��
��ͼ����֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=1���������߾���A��-1��0����C��0��-3�����㣬��x�ύ����һ��B�� ��ͼ����֪������y=ax2+bx+c�Ķ����ǣ�-1��-4��������x�ύ��A��B��1��0�����㣬��y���ڵ�C��
��ͼ����֪������y=ax2+bx+c�Ķ����ǣ�-1��-4��������x�ύ��A��B��1��0�����㣬��y���ڵ�C��