Question

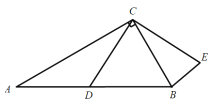
【题目】已知∠MCN＝45°，点B在射线CM上，点A是射线CN上的一个动点（不与点C重合）．点B关于CN的对称点为点D，连接AB、AD和CD，点F在直线BC上，且满足AF⊥AD．小明在探究图形运动的过程中发现AF＝AB：始终成立．

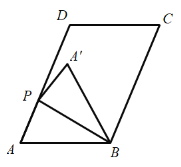
如图，当0°＜∠BAC＜90°时．

① 求证：AF＝AB；

② 用等式表示线段与之间的数量关系，并证明；

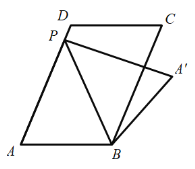
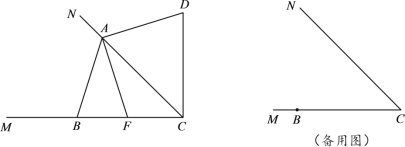
当90°＜∠BAC＜135°时，直接用等式表示线段CF、CD与CA之间的数量关系是 ．

Answer 1

【答案】①证明过程见解析，②CD+CF＝AC，过程见解析； ．

【解析】

①过点A作AG⊥BC于G，作AH⊥CD于H，判断出四边形AGCH是矩形，得出∠GAH=90°，得出∠FAG=∠DAH，进而判断出△FAG≌△DAH，即可得出结论； ②由矩形AGCH是正方形，判断出CH=CG，∠CAH=∠DCA=45°，由①知，△AGF≌△AHD，得出FG=DH，即CH=，再根据勾股定理得，AC= CH，即可得出结论；

同（1）的方法判断出△AHD≌AGF，得出DH=FG，进而得出CH=，即可得出结论．

解：（1）①如图1， ∵点D，B关于CD对称，

∴AB=AD，∠BAC=∠DAC，∠ACD=∠MCN=45°，

∴∠DCM=90°，

过点A作AG⊥BC于G，作AH⊥CD于H，

∴AG=AH，∠AGC=∠AHC=∠DCM=90°，

∴四边形AGCH是矩形，

∴∠GAH=90°，

∵AF⊥AD，

∴∠FAD=90°，

∴∠FAG=∠DAH，

∴△AGF≌△AHD（ASA），

∴AF=AD，

∵AB=AD，

∴AF=AB；

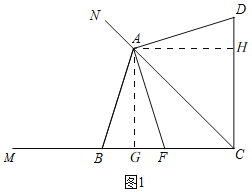
②结论：CD+CF=AC， 理由：由①知，四边形AGCH是矩形，AG=AH，

∴矩形AGCH是正方形，

∴CH=CG，∠CAH=∠DCA=45°，

由①知，△AGF≌△AHD，

∴FG=DH，

∴CD+CF=CH+DH+CG-FG=2CH，

∴CH=，

根据勾股定理得，AC=CH=，

∴CD+CF＝；

（2）结论：CD-CF=AC， 理由：如备用图， 同（1）的方法得，△AHD≌AGF，

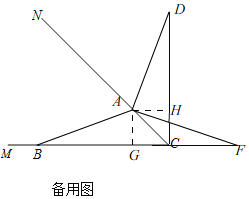
∴DH=FG，

∴CD-CF=CH+DH-FG+CG=2CH，

∴CH=，

根据勾股定理得，AC=CH=，

∴CD-CF=AC，

故答案为：CD-CF=AC．