题目内容
(本题12分)在正方形网格 中以点
中以点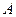 为圆心,
为圆心,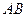 为半径作圆
为半径作圆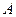 交网格于点
交网格于点 (如图(1)),过点
(如图(1)),过点 作圆的切线交网格于点
作圆的切线交网格于点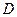 ,以点
,以点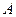 为圆心,
为圆心,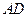 为半径作圆交网格于点
为半径作圆交网格于点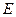
(如图(2)).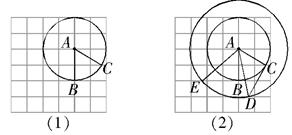
|
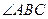 的度数;
的度数;(2)求证:

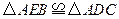 ;
;(3)
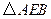 可以看作是由
可以看作是由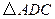 经过怎样的变换得到的?并判断
经过怎样的变换得到的?并判断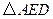 的形状(不用说明理由).
的形状(不用说明理由).(4)如图(
 3),已知直线
3),已知直线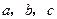 ,且a∥b,b∥c,在图中用
,且a∥b,b∥c,在图中用 直尺、三角板、圆规画等边三角形
直尺、三角板、圆规画等边三角形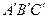 ,使三个顶点
,使三个顶点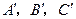 ,分别在直线
,分别在直线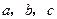 上.要求写出简要的画图过程,不需要说明理由.
上.要求写出简要的画图过程,不需要说明理由.
(1)连接BC,由网格可知点C在AB的中垂线上,
∴AC=BC,…………………………………………………………………………………1分
∵AB=AC,
∴AB=BC=AC,即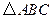 是等边三角形.……………………………………………2分
是等边三角形.……………………………………………2分
∴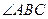 =60°;…………………………………………………………………………3分
=60°;…………………………………………………………………………3分
(2)∵CD切⊙A于点C,
∴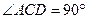
 .…………………………………………………………………4分
.…………………………………………………………………4分
在Rt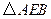 与Rt
与Rt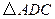 中,
中,
∵AB=AC,AE=AD.……………………………………………………………………5分
∴ (HL).……………………………………………………6分
(HL).……………………………………………………6分
(3)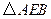 可以看作是由
可以看作是由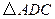 绕点A顺时针旋转60°得到的.…………7分
绕点A顺时针旋转60°得到的.…………7分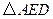 是等边三角形.………………………………………………………………8分
是等边三角形.………………………………………………………………8分
(4)在直线a上任取一点,记为点A′,作A′M′⊥b,垂足为点M′;作线段
A′M′的垂直平分线,此直线记为直线d;以点A′为圆心,A′M′长为半径画圆,与直线d交于点N′;………………………9分
过点N′作N′C′⊥A′N′交直线c于点C′;……………………………………10分
以点A′为圆心,A ′C′长为半径画圆,此圆交直线b于点B′;……………11分
连接A′B′、B′C′,则△A′B′C′为所求等边三角形.………………………12分
解析

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
(本题12分)在正方形网格中以点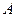 为圆心,
为圆心,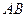 为半径作圆
为半径作圆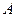 交网格于点
交网格于点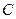 (如图(1)),过点
(如图(1)),过点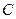 作圆的切线交网格于点
作圆的切线交网格于点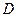 ,以点
,以点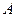 为圆心,
为圆心,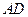 为半径作圆交网格于点
为半径作圆交网格于点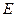
(如图(2)).
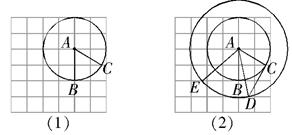
问题:(1)求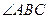 的度数;
的度数;
(2)求证: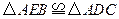 ;
;
(3)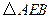 可以看作是由
可以看作是由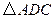 经过怎样的变换得到的?并判断
经过怎样的变换得到的?并判断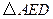 的形状(不用说明理由).
的形状(不用说明理由).
(4)如图(3),已知直线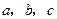 ,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形
,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形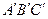 ,使三个顶点
,使三个顶点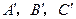 ,分别在直线
,分别在直线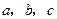 上.要求写出简要的画图过程,不需要说明理由.
上.要求写出简要的画图过程,不需要说明理由.

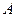 为圆心,
为圆心,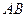 为半径作圆
为半径作圆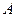 交网格于点
交网格于点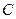 (如图(1)),过点
(如图(1)),过点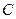 作圆的切线交网格于点
作圆的切线交网格于点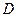 ,以点
,以点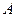 为圆心,
为圆心,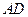 为半径作圆交网格于点
为半径作圆交网格于点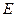
(如图(2)).

|
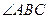 的度数;
的度数;(2)求证:
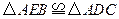 ;
;(3)
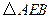 可以看作是由
可以看作是由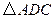 经过怎样的变换得到的?并判断
经过怎样的变换得到的?并判断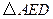 的形状(不用说明理由).
的形状(不用说明理由).(4)如图(3),已知直线
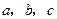 ,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形
,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形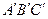 ,使三个顶点
,使三个顶点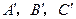 ,分别在直线
,分别在直线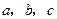 上.要求写出简要的画图过程,不需要说明理由.
上.要求写出简要的画图过程,不需要说明理由.
 为圆心,
为圆心,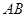 为半径作圆
为半径作圆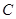 (如图(1)),过点
(如图(1)),过点 ,以点
,以点 为半径作圆交网格于点
为半径作圆交网格于点
 ,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形
,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形 ,使三个顶点
,使三个顶点 ,分别在直线
,分别在直线 为圆心,
为圆心, 为半径作圆
为半径作圆 (如图(1)),过点
(如图(1)),过点 ,以点
,以点 为半径作圆交网格线于点
为半径作圆交网格线于点 (如图(2)).
(如图(2)).
 的度数;
的度数; ;
; 可以看作是由
可以看作是由 经过怎样的变换得到的?并判断
经过怎样的变换得到的?并判断 的形状(不用说明理由).
的形状(不用说明理由). ,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形
,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形 ,使三个顶点
,使三个顶点 ,分别在直线
,分别在直线
 为圆心,
为圆心, 为半径作圆
为半径作圆 (如图(1)),过点
(如图(1)),过点 ,以点
,以点 为半径作圆交网格线于点
为半径作圆交网格线于点 (如图(2)).
(如图(2)).
 的度数;
的度数; ;
; 可以看作是由
可以看作是由 经过怎样的变换得到的?并判断
经过怎样的变换得到的?并判断 的形状(不用说明理由).
的形状(不用说明理由). ,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形
,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形 ,使三个顶点
,使三个顶点 ,分别在直线
,分别在直线